Question

In the circuit diagram shown, ${X_c} = 100\;{\rm{\Omega }}$, ${X_L} = 200\;{\rm{\Omega }}$, $R = 100\;{\rm{\Omega }}$. The effective current through the source is:

(A) $2\;{\rm{A}}$
(B)$2\sqrt 2 \;{\rm{A}}$
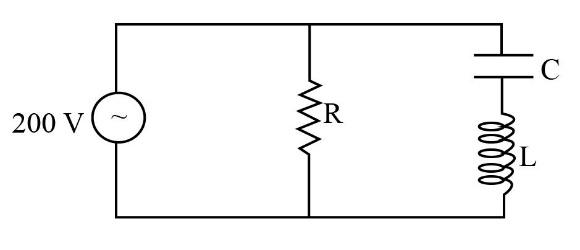
(C) $0.5\;{\rm{A}}$
(D) $\sqrt {0.4} \;{\rm{A}}$

Answer 1

This question involves the concept of alternating current, impedance, and net reactance. In the question you are required to calculate the effective current, which can be evaluated by calculating the effective impedance of the LC-circuit first. After this, you will be required to calculate the net reactance. In the end, you can calculate the current by applying ohm’s law.

Complete step by step answer:
Given
The capacitive reactance is ${X_c} = 100\;{\rm{\Omega }}$.
The inductive reactance is ${X_L} = 200\;{\rm{\Omega }}$.
The resistance of the resistor is $R = 100\;{\rm{\Omega }}$.
The voltage is $V = 200\;{\rm{V}}$.

As we know that the expression for the effective impedance of series LC-circuit is given as,
$X = {X_l} - {X_c}$

Now we substitute the values of both capacitive and inductive reactance in above expression,
$X = 200\;{\rm{\Omega }} - 100\;{\rm{\Omega }}$

As the resistance is in parallel combination with the effective impedance. So, the expression for the net reactance is given as,
$\dfrac{1}{{z'}} = \sqrt {{{\left( {\dfrac{1}{R}} \right)}^2} + {{\left( {\dfrac{1}{X}} \right)}^2}}$

Now we substitute the values in the above expression, to get the value of net reactance,
$\dfrac{1}{{z'}} = \sqrt {{{\left( {\dfrac{1}{{100\;{\rm{\Omega }}}}} \right)}^2} + {{\left( {\dfrac{1}{{100\;{\rm{\Omega }}}}} \right)}^2}} \\\ \implies \dfrac{1}{{z'}} = \sqrt {\dfrac{1}{{10000\;{\rm{\Omega }}}} + \dfrac{1}{{10000\;{\rm{\Omega }}}}} \\\ \implies \dfrac{1}{{z'}} = \sqrt {\dfrac{1}{{5000}}} \\\ \implies z' = 50\sqrt 2 \;{\rm{\Omega }}$

We know that the expression for the effective current is given as,
$I = \dfrac{V}{{z'}}$

We substitute the values in the above expression,
$I = \dfrac{{200\;{\rm{V}}}}{{50\sqrt 2 \;{\rm{\Omega }}}}\\\ \implies I = 2\sqrt 2 \;{\rm{A}}$

Therefore, the effective current thought the source is $2\sqrt 2 \;{\rm{A}}$.

Note:
You can face problems in the calculation part of net reactance and effective impedance. Another method to approach this question would be first calculating the current through the resistance, which would be $2\;{\rm{A}}$. Then we can calculate the total current passing through the LC circuit, which would also be $2\;{\rm{A}}$. In the end, we can calculate the resultant current for both effective impedance and resistor, which would be $2\sqrt 2 \;{\rm{A}}$.