Question

In the circuit diagram of Zener diode as shown in figure, when the value of ${V_0}$ is $8$ volt, the current through the Zener diode is ${i_1}$ and when ${V_0}$ is $16$ volt, the corresponding current is ${i_2}$ . Find the value of ( ${i_1} - {i_2}$ ). Zener breakdown voltage ${V_2}$ equals $6\,{\text{V}}$ .

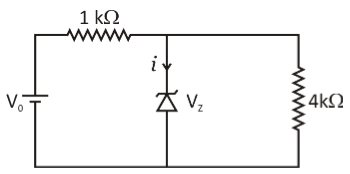
A. Zero
B. $5.0\,{\text{mA}}$
C. $1.5\,{\text{mA}}$
D. $8\,{\text{mA}}$

Answer 1

First of all, we will draw the circuit for the two cases. One is for $8$ volt and the other is for $16$ volt. After that we will use Ohm’s law to find the current flowing through the load followed by Zener diode for the two cases. Lastly, we subtract the magnitudes of currents as directed.

Formula used:
Ohm’s law is given as:
$i = \dfrac{V}{R}$ …… (1)
Where,
$i$ indicates the current.
$V$ indicates voltage.
$R$ indicates resistance.

Complete step by step answer:
In the given question, we are supplied with the following data:
A Zener diode is connected as shown in the figure in the question.The current through the Zener diode is ${i_1}$ when the value of ${V_0}$ is $8$ volt.Again, the current through the Zener diode is ${i_2}$ when the value of ${V_0}$ is $16$ volt. We are asked to find the value of the current ( ${i_1} - {i_2}$ ).We are also given that Zener breakdown voltage ${V_2}$ equals $6\,{\text{V}}$ .

To begin with, we will draw the diagrams. For the first case, for the voltage of $8$ volt and we will try to find out the value of ${i_1}$ .

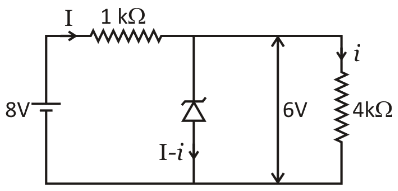
There is a property of Zener breakdown, for which the voltage across the Zener diode will be $6$ volt. The current flowing through the Zener diode is $I - i$ . The current flowing through the $4\,{\text{k}}\Omega$ is $i$ .Now, the current through the $4\,{\text{k}}\Omega$ is:
i = \dfrac{6}{{4 \times {{10}^3}}} \\\ \Rightarrow i = 1.5 \times {10^{ - 3}}\,{\text{A}} \\\ \Rightarrow i = 1.5\,{\text{mA}} \\\
The voltage across the $1\,{\text{k}}\Omega$ resistor is:
\left( {8 - 6} \right)\,{\text{V}} \\\ \Rightarrow 2\,{\text{V}} \\\
So, the current flowing through the $1\,{\text{k}}\Omega$ resistor is:
I = \dfrac{2}{{1 \times {{10}^3}}} \\\ \Rightarrow i = 2 \times {10^{ - 3}}\,{\text{A}} \\\ \Rightarrow i = 2\,{\text{mA}} \\\
So,
${i_1} = I - i \\\ \Rightarrow {i_1} = 2 - 1.5 \\\ \Rightarrow {i_1} = 0.5\,{\text{mA}}$

For the second case,
For the voltage of $16$ volt and we will try to find out the value of ${i_2}$ .

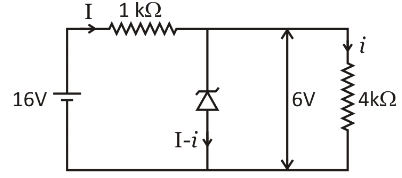
The current through the $4\,{\text{k}}\Omega$ resistor will remain the same which is $1.5\,{\text{mA}}$ .The voltage across the $1\,{\text{k}}\Omega$ resistor is:
\left( {16 - 6} \right)\,{\text{V}} \\\ \Rightarrow 10\,{\text{V}} \\\
So, the current flowing through the $1\,{\text{k}}\Omega$ resistor is:
I = \dfrac{{10}}{{1 \times {{10}^3}}} \\\ \Rightarrow i = 10 \times {10^{ - 3}}\,{\text{A}} \\\ \Rightarrow i = 10\,{\text{mA}} \\\
So,
{i_2} = I - i \\\ \Rightarrow {i_2} = 10 - 1.5 \\\ \Rightarrow {i_2} = 8.5\,{\text{mA}} \\\
Now, we can find the difference of the currents for the two different voltages.
${i_2} - {i_1} \\\ \Rightarrow 8.5 - 0.5 \\\ \therefore 8\,{\text{mA}}$
Hence, the answer is $8\,{\text{mA}}$ .

The correct option is D.

Note: While solving the problem, we should remember that the breakdown voltage of an insulator is the minimal voltage that allows a component of an insulator to become electrically conductive. The breakdown voltage is the minimum reverse voltage for diodes that lets the diode conduct in reverse appreciably. In this problem, most of the students fail to assign the voltage of ${\text{6}}$ volts to the Zener diode. It is because the Zener breakdown occurs at ${\text{6}}$ volts.