Question
Question: -In the circuit Diagram is given below find A. A total resistance of the circuit B. Total curren...
-In the circuit Diagram is given below find
A. A total resistance of the circuit
B. Total current flowing in the circuit
C. The potential difference across R1
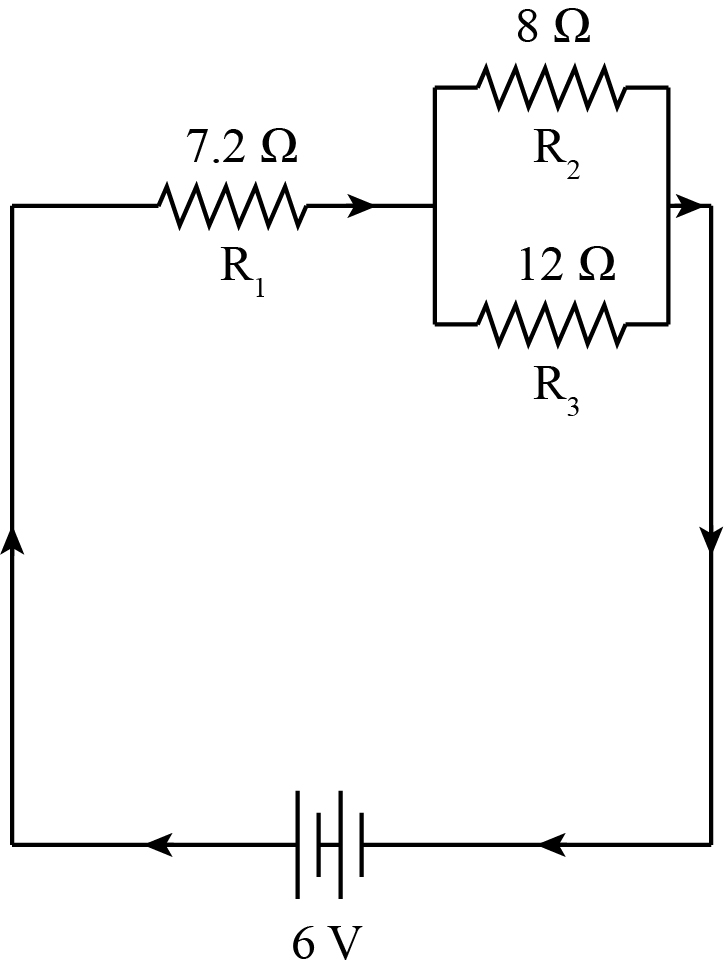
Solution
The circuit is made up of resistances in series and parallel. So we will use the formula of equivalent resistances in series and parallel. R2 and R3 are connected parallelly. First, we will solve the Equivalent resistance for these two R2 and R3 Resistances. Now the new calculated equivalent resistance is in series with the resistance R1. In this way, the total equivalent resistance will be calculated for the circuit.
Complete step by step answer:
When the resistances are in parallel combination, then the voltage difference across all the resistance is the same, but the current is different through the resistances. And when the resistances are in series connection, then the same current flows through all the resistances, but the voltage difference across all the resistance is different.
A) First, we calculate the equivalent resistance in the parallel combination. In parallel combination, the reciprocal of equivalent resistance is the sum of the reciprocals of resistance in parallel.
Rp.eq1=R21+R31
Now, putting the value of R2 and R3 to find out Rp.eq
Rp.eq1=81+121 ⇒Rp.eq=243+2 ⇒Rp.eq=245Ω
Hence, Rp.eq=524Ω
Now we will calculate the equivalent resistance ofRp.eq andR1 which is in series combination now. And in series combination, the equivalent resistance is calculated by adding all the resistances in series.
So, R=R1+Rp.eq
Now, putting the value of R1 andRp.eq to find out R.
R=7.2+524 ⇒R=7.2+4.8 ⇒R=13Ω
B) The total current flowing in the circuit can be obtained from the Ohm’s Law.
The total current I=RV
Putting the value of V and R in the current expression.
I=136 ⇒I=0.461A
C) The potential difference acrossR1is,
V1=IR1 (According to the Ohm’s law)
Putting the value of I And R1in the above expression,
V1=0.461×7.2 ⇒V1=3.32Volt
The given circuit is hence can be converted into a circuit have only one resistance and a current flowing in it.
Note:
You can go wrong while calculating the equivalent resistance for series and parallel because sometimes the circuits are very complicated to understand which resistances are in parallel and which are in series.
