Question
Question: In the circuit diagram given below five resistances of \(10\Omega\), \(40\Omega \), \(30\Omega \), \...
In the circuit diagram given below five resistances of 10Ω, 40Ω, 30Ω, 20Ω and 60Ω are connected as shown to a 12V battery.Calculate total resistance in the circuit and net current drawn from the battery.
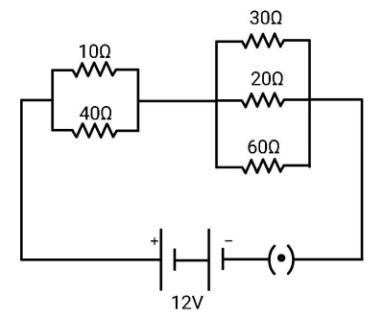
Solution
We are supposed to find the total resistance of the circuit, meaning that, we will find such a value of single resistance which will provide equal resistance that is offered by this combination of resistances. Here, you can see five resistors are present, find the series and parallel combination of these resistances and reduce it to a single resistance. This single resistance will be the total resistance. To find the current, use Ohm’s Law.
Complete step by step answer:
To identify series and parallel, one always looks for the end points of the resistors. Consider two resistors. If only one end of both the resistors are connected to the same point, then the resistors are in series. If both the ends of both resistors are connected to the same point, then the resistors are in parallel. For a clear understanding, let us try labelling the ends. Let the resistors have resistances R1 and R2. Let the ends of resistor R1 be denoted by points A and B and that of resistor R2 be denoted by C and D.
We say that, when the points A and C are connected to some point X and the points B and D are connected to some other point Y, the resistors are connected in parallel. Orientation in resistors doesn’t matter, so there is no need for different combinations of end points. Now, let us look for series and parallel combinations of resistances in the circuit. You can see that the resistors 10Ω and 40Ω are in parallel and the resistors 30Ω, 20Ω and 60Ω are in parallel combination. When the resistances are connected in parallel combination, the equivalent resistance will be equal to reciprocal of sum of reciprocals. Mathematically,
Reff=R11+R21+R31+....1
So, the equivalent resistance of 10Ω and 40Ω will be 101+4011=8Ω and equivalent resistance of 30Ω, 20Ω and 60Ω will be 301+201+6011=10Ω.
Now, the circuit is reduced and it can be seen as a series combination of equivalent resistances 8Ω&10Ω. When the resistors are connected in series, the equivalent will be simply the sum of the resistances. Therefore, Req=10+8=18Ω. The resistance of the circuit is 18Ω.
Using Ohm’s Law, we have V=IR where V is the applied voltage, I is the current and R is the resistance. Here, we have V=12V, R=18Ω.
Therefore, I=RV=1812=32A.
Hence, total resistance in the circuit is 18Ω and net current drawn from the battery is 32A.
Note: Remember the method of determining the combination in which the resistances are connected, whether they are in series, or in parallel or it is a combination of series and parallel. Also remember Ohm’s Law which gives the relation between current, potential difference (voltage) and resistance.
