Question

In the circuit, as shown in a figure if all the symbols have their usual meaning, then identify the correct statement,

$A.{\text{ }}{q_2} = {q_2};{V_2} = {V_3}$
$B.{\text{ }}{q_1} = {q_2}\; + {q_3};{V_2} = {V_3}$
$C.{\text{ }}{q_1} = {q_2}\; + {q_3};{V_1}\; + {V_2}\; + {V_3}$
$D.{\text{ }}{q_1}\; + {q_2} + {q_3} = 0;{V_2}\; = {V_3} = V - {V_1}$

Answer 1

Hint A Capacitor is a device that stores electrical energy in an electric field. It is a passive electronic component with two terminals. The net charge on the capacitor is always zero because there is equal and unlike charges on plates.
Formula Used: We will be using the relation of Capacitance $C = \dfrac{q}{V}$

Complete step by step answer:
The flow of electrons onto the plates is known as the capacitor charging current which continues to flow until the voltage across both plates is equal to the applied voltage. At this point the capacitor is said to be fully charged with electrons. The amount of potential difference present across the capacitor depends upon how much charge was deposited onto the plates by the work being done by the voltage source and how much capacitance the capacitor has.
Capacitors in Series: When capacitors are connected one after another, they are said to be in series. Two or more capacitors in series will always have equal amounts of coulomb charge across their plates. As the charge q is equal and constant, the voltage drop across the capacitor is determined by the value of the capacitor and the voltage source. The total charge q is the sum of the individual charge.

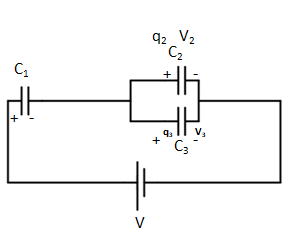
${q_1} = {q_2}\; + {q_3}$
As ${C_1}$ and combine (${C_{2,}}{C_3}$) are in series so charge on ${C_1} =$ the charge on (${C_{2,}}{C_3}$ )
Therefore, Charge on the capacitor $1$ is equal to Charge on the capacitor $2$ and $3$
${q_1} = {q_2} + \;{q_3}$
As ${C_2}and{C_3}$ are in parallel so potential across each is the same. Therefore${V_2} = {V_3}$
Here, $V = {V_1}\; + {V_2}$ or $V = {V_1}\; + {V_3}$
Capacitors in series: ${q_1} = {q_2} + \;{q_3}$
Capacitors in parallel: ${V_2} = {V_3}$
Option; B) ${q_1} = {q_2}\; + {q_3};{V_2} = {V_3}$

NOTE: It is an electrical energy storing device. The capacitors vary widely, but all contain at least two electrical conductors [plates] separated by a dielectric [insulator].