Question
Question: in the case of a simple pendulum, a graph has been represented between its kinetic energy, KE and it...
in the case of a simple pendulum, a graph has been represented between its kinetic energy, KE and its potential energy, PE against displacement d. Identify which one of the following is best representing these correctly? (Graph is schematic and not drawn to scale)
A.
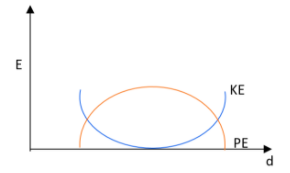
B.
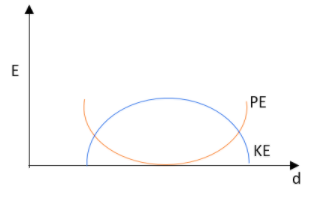
C.
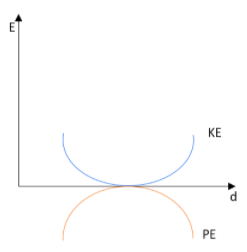
D.
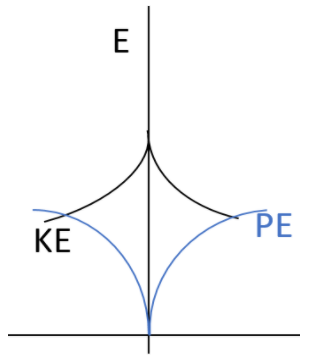
Solution
The kinetic energy in a simple harmonic motion can be found by taking the half of the product of the mass and square of the velocity. Using this find out the variation in potential energy and kinetic energy with a displacement. This will help you in answering this question.
Complete answer:
The kinetic energy in a simple harmonic motion can be found by taking the half of the product of the mass and square of the velocity. That is we can write that,
KE=21mu2
Where u be the velocity. The velocity of the simple pendulum in a SHM can be shown as,
u=(A2−x2)ω2
Substituting this in the equation of kinetic energy will give,
KE=21m(A2−x2)ω2
As we all know the spring constant can be found as,
K=mω2
Substituting this value in the equation will give,
KE=21K(A2−x2)
For a simple pendulum, the variation in kinetic energy and potential energy with displacement d will be,
