Question

In the below figure, Two concentric circles of radii “a” and “b” (a > b) are given. Find the length of the chord AB of the larger circle which touches the smaller circle at point C.

Answer 1

In the above figure, given in the problem, we have to find the length of AB. Now, as you can see, OC is the perpendicular from the centre of the chord of the larger circle and we know that the perpendicular from the centre of the circle onto a chord bisects the chord. This means that $AC=CB$. From the figure, you can see that. Triangle OCB is a right-angled triangle, right-angled at C. In this triangle, OC is equal to “b” and OB equals “a” so we can find the length of CB by using Pythagoras theorem which states that ${{\left( Hypotenuse \right)}^{2}}={{\left( Perpendicular \right)}^{2}}+{{\left( Base \right)}^{2}}$. Now, the length of AB is equal to twice of CB.

Complete step by step answer:
We have given the following figure in the above problem:

Let us mark the smaller radius as “b” and the larger radius as “a” in the above diagram.

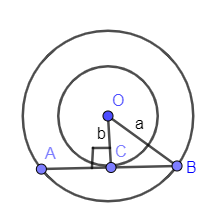
In the above problem, we are asked to find the length of the chord AB of the larger circle which touches the smaller circle at point C.
It is given that OC is perpendicular to AB. And we know that if a perpendicular from the centre of the circle drops onto the chord then that perpendicular bisects the chord. So, the length of AC and CB are equal.
$AC=CB$
As you can see the right-angled triangle OCB in the above figure in which we know the length of OB as “a” and OC as “b”. But we don’t know the length of CB which we can calculate by using the Pythagoras theorem.
In Pythagoras theorem, we have:
${{\left( Hypotenuse \right)}^{2}}={{\left( Perpendicular \right)}^{2}}+{{\left( Base \right)}^{2}}$
Now, hypotenuse is OB, perpendicular is OC and base is CB so substituting them in the above equation we get,
${{\left( OB \right)}^{2}}={{\left( OC \right)}^{2}}+{{\left( CB \right)}^{2}}$
Substituting OB as “a”, OC as “b” in the above equation we get,
$\begin{aligned} & {{\left( a \right)}^{2}}={{\left( b \right)}^{2}}+{{\left( CB \right)}^{2}} \\\ & \Rightarrow {{\left( CB \right)}^{2}}={{\left( a \right)}^{2}}-{{\left( b \right)}^{2}} \\\ \end{aligned}$
Taking square root on both the sides we get,
$CB=\sqrt{{{a}^{2}}-{{b}^{2}}}$
Now, the length of AB is equal to the addition of AC and CB.
$AB=AC+CB$
And we have shown above that $AC=CB$ so using this relation in the above equation we get,
$\begin{aligned} & AB=CB+CB \\\ & \Rightarrow AB=2CB \\\ \end{aligned}$
Substituting $CB=\sqrt{{{a}^{2}}-{{b}^{2}}}$ in the above equation we get,
$AB=2\sqrt{{{a}^{2}}-{{b}^{2}}}$
Hence, we got the length of the chord AB touching the smaller circle at point C as $2\sqrt{{{a}^{2}}-{{b}^{2}}}$.

Note: In the above problem, the tricky part is the property that, if a perpendicular is dropped on the chord of the circle then that perpendicular bisects the chord. Pythagoras theorem is used very often in the problems but this property of the circle is specific to some problems. So, this question will make you realize the importance of this property.
The other point is in the above solution, in the following step:
$AB=AC+CB$
$\begin{aligned} & AB=CB+CB \\\ & \Rightarrow AB=2CB \\\ \end{aligned}$
You might have thought about why we put CB in place of AC and not AC in place of CB. The answer is because we have calculated the value of CB from the Pythagoras theorem so we know the value of CB not AC.