Question
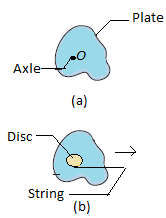
Question: In the below figure (a), an irregularly shaped plastic plate with uniform thickness and density (mas...
In the below figure (a), an irregularly shaped plastic plate with uniform thickness and density (mass per unit volume) is to be rotated around an axle that is perpendicular to the plate face and through point O. The rotational inertia of the plate about that axle is measured with the following method. A circular disc of mass 0.500kg and radius 2.0cm is glued to the plate, with its center aligned with point O (Fig.b). A string is wrapped around a top. Then the string is wrapped around a top. Then the string is pulled for 5.00s. As a result the disk and plate are rotated by a constant force of 0.400N that is applied by the string tangentially to the edge of the disc. The resulting angular speed is 114rad/s. What is the rotational inertia of the plate about the axle?
Solution
Determine the angular acceleration of the system of the disc and plate. Determine the moment of inertia of the disc about its centre. Use the formula for the torque acting on an object due to a force and in terms of the angular acceleration of the object and determine the moment of inertia of the disc-plate system. Finally subtract the moment of inertia of the disc from moment of inertia of disc-plate system.
Formula used:
The angular acceleration of an object is
α=tω …… (1)
Here, ω is the angular speed of the object and t is time.
The torque τ acting on an object due to the force F is
τ=Fr …… (2)
Here, r is the perpendicular distance between the point of action of the force and the centre of the torque.
The torque τ on an object is
τ=Iα …… (3)
Here, I is the moment of inertia of the object and α is the angular acceleration of the object.
The moment of inertia Idisc of the disc about its centre is
Idisc=21MR2 …… (4)
Here, M is the mass of the disc and R is the radius of the disc.
Complete step by step solution:
We have given that the mass of the disc is 0.500kg and the radius of the disc is 2.0cm.
M=0.500kg
R=2.0cm
The angular speed of the disc-plate system is 114rad/s and the string is pulled for time 5.00s.
ω=114rad/s
t=5.00s
The force acting on the system is 0.400N.
F=0.400N
Let us first determine the angular acceleration of the disc-plate system using equation (1).
Substitute 114rad/s for ω and 5.00s for t in equation (1).
α=5.00s114rad/s
⇒α=22.8rad/s2
Now determine the moment of inertia of the disc about its centre at point O using equation (4).
Substitute 0.500kg for M and 2.0cm for R in equation (4).
Idisc=21(0.500kg)(2.0cm)2
⇒Idisc=21(0.500kg)[(2.0cm)(1cm10−2m)]2
⇒Idisc=1×10−4kg⋅m2
The perpendicular distance between the point of action of the force F and centre of torque O is equal to the radius R of the disc.
Substitute Iα for τ and R for r in equation (2).
Iα=FR
⇒I=αFR
Here, I is the moment of inertia of the disc-plate system.
Substitute 0.400N for F, 2.0cm for R and 22.8rad/s2 for α in the above equation.
⇒I=22.8rad/s2(0.400N)(2.0cm)
⇒I=22.8rad/s2(0.400N)[(2.0cm)(1cm10−2m)]
⇒I=3.5×10−4kg⋅m2
Hence, the moment of inertia of the disc-plate system is 3.5×10−4kg⋅m2.
The moment of inertia I of the disc-plate system is equal to sum of moment of inertia Iplate of the plate and moment of inertia Idisc of disc about point O.
I=Iplate+Idisc
Rearrange the above equation for Iplate.
Iplate=I−Idisc
Substitute 3.5×10−4kg⋅m2 for I and 1×10−4kg⋅m2 for Idisc in the above equation.
Iplate=(3.5×10−4kg⋅m2)−(1×10−4kg⋅m2)
⇒Iplate=2.5×10−4kg⋅m2
Hence, the rotational inertia of the plate about the axle is 2.5×10−4kg⋅m2.
Note:
The students should not forget that the moment of inertia obtained by equating two torques equations is the moment of inertia of the disc-plate system and not the required moment of inertia of the plate. The students should also not forget to convert the unit of radius of the disc in the SI system of units.
