Question

In the below diagram, we have to find the angle $\alpha$ ?

Answer 1

Hint : In the above figure, we have to calculate the angle $\alpha$ which we are going to calculate by first of all find the angle $\beta$ which can be calculated by using $\tan \beta$ in $\Delta DEC$ . We know that $\tan \beta =\dfrac{\text{Perpendicular}}{\text{Base}}$ here substitute perpendicular is 21 and base is 50. Now, we know angle $\beta$ and angle CDE is ${{90}^{\circ }}-\beta$ . And line ADB is forming a linear pair so summation of angle ADC and CDB is ${{180}^{\circ }}$ and from this linear pair we can get angle CDB. Now, we already know angle CDE and angle CDB so from this we can find angle EDB. Now, $\Delta DEB$ is a right triangle, we have calculated angle EDB, angle DEB is given as ${{90}^{\circ }}$ so from the summation of all angles of triangle as ${{180}^{\circ }}$ we can find angle $\alpha$ .

Complete step-by-step answer :
The below figure is given in the above question.

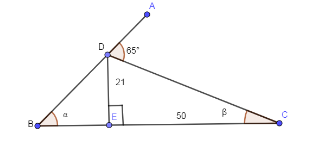
We are asked to find angle $\alpha$ in the above figure.
First of all, we are going to find angle $\beta$ . As we can see that $\Delta DEC$ is a right triangle and using the trigonometric ratios we can find angle $\beta$ by using $\tan \beta$ .

We know that,
$\tan \beta =\dfrac{\text{Perpendicular}}{\text{Base}}$
In the above figure, perpendicular is 21 and base is 50 so substituting these values in the above equation we get,
$\tan \beta =\dfrac{21}{50}$
Taking ${{\tan }^{-1}}$ on both the sides we get,
$\beta ={{\tan }^{-1}}\left( \dfrac{21}{50} \right)$
From the given figure, we can see that ADB is a linear pair so the sum of angles lying on this line is ${{180}^{\circ }}$ .

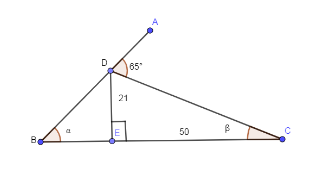
Adding all the angles lie on the straight line ADB we get,
$\begin{aligned} & \angle ADC+\angle CDE+\angle EDB={{180}^{\circ }} \\\ & \Rightarrow {{65}^{\circ }}+\angle CDE+\angle EDB={{180}^{\circ }} \\\ \end{aligned}$
Subtracting ${{65}^{\circ }}$ on both the sides we get,
$\begin{aligned} & \angle CDE+\angle EDB={{180}^{\circ }}-{{65}^{\circ }} \\\ & \Rightarrow \angle CDE+\angle EDB={{115}^{\circ }} \\\ \end{aligned}$
Now, $\angle CDE={{90}^{\circ }}-\beta$ so substituting this angle in the above equation we get,
$\begin{aligned} & {{90}^{\circ }}-\beta +\angle EDB={{115}^{\circ }} \\\ & \Rightarrow \angle EDB={{115}^{\circ }}-{{90}^{\circ }}+\beta \\\ & \Rightarrow \angle EDB={{25}^{\circ }}+\beta \\\ \end{aligned}$
Now, $\Delta DEB$ is a right triangle so angle $\alpha$ is equal to ${{90}^{\circ }}-\angle EDB$ we get,
$\alpha ={{90}^{\circ }}-\angle EDB$
Substituting the value of angle EDB from the above equations we get,
$\begin{aligned} & \alpha ={{90}^{\circ }}-\left( {{25}^{\circ }}+\beta \right) \\\ & \Rightarrow \alpha ={{65}^{\circ }}-\beta \\\ \end{aligned}$
Substituting the value of angle $\beta ={{\tan }^{-1}}\left( \dfrac{21}{50} \right)$ we get,
$\alpha ={{65}^{\circ }}-{{\tan }^{-1}}\left( \dfrac{21}{50} \right)$
Hence, we have got the value of $\alpha$ as ${{65}^{\circ }}-{{\tan }^{-1}}\left( \dfrac{21}{50} \right)$ .

Note : The question demands the knowledge of trigonometric ratios like what is $\tan \beta$ in the right triangle and what is a linear pair. And the sum of all the angles of a triangle are ${{180}^{\circ }}$. Missing any information will paralyze you in solving this problem. In this question, possibilities of calculation mistakes are pretty high so be careful while writing all the steps in the solution.