Question
Question: In the balance Meter Bridge, the resistance of bridge wire is \(0.1\Omega /cm\). Unknown resistance ...
In the balance Meter Bridge, the resistance of bridge wire is 0.1Ω/cm. Unknown resistance X connected in the left gap and 6Ω in the right gap, null point divides the wire in the ratio 2:3. Find the current drawn from the battery of 5V having negligible resistance.
A. 1A
B. 1.5A
C. 2A
D. 5A
Solution
We have provided with balance Meter Bridge, which has null point divides wire in 2:3 ratio, hence calculate length of wires l1 and l2 which is divided into five parts apply balance condition of wheatstone network and calculate value of unknown resistance. Then use Kirchhoff’s second law to calculate the value of current flows through the circuit.
Complete step by step answer:
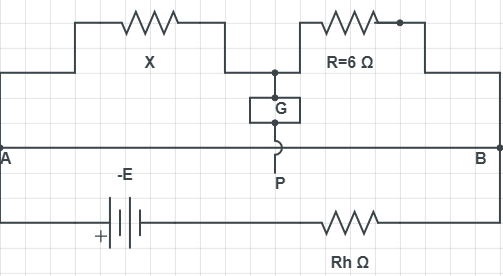
We have a Meter Bridge which balances the total resistance of bridge wire is 0.1Ω/cm. X is the total resistance which is connected to the left gap and R=6Ω in the right gap. Null point is dividing wire in 2:3 ratios. A battery 5V having negligible resistance is also connected to circuit. Now we need to calculate. Consider Current drawn from the 5V battery.
We know that the Meter Bridge has a resistance of 0.1Ω/cm and its total length of wire is always 1m i.e., 100cm. So, resistance of wire (RW) is given by,
RW=0.1×100RW=10Ω
We have given wire AB is divided into 2:3 ratios. I.e. two part from A to P and tree parts from P to B. Now if we divide 10Ω resistance in this wire the length of AP is given by,
l1=10×52=4
(We have total five parts and l1 are the length contains two parts out of five parts) Similarly for length PB is given by,
l2=10×53=6
(We have total five parts and l2 are the length contains three parts out of five parts)
It is given that the Meter Bridge is a balanced network or circuit and we get null points at P, we know that, in a balanced condition even though current flows in the rest of circuit, the galvanometer will not show any deflection. I.e. it shows a null point. So according to balance condition of Wheatstone network, we have,
RX=l2l1
Where, X= unknown resistance
6X=64∴X=4Ω
Hence unknown resistance (X) is 4Ω.
Now let’s find current, we know that current drawn from 5V is given by,
I=ReqV.......(1)
To find equivalent resistance:
If we consider resistance across a point A and B then circuit looks like,
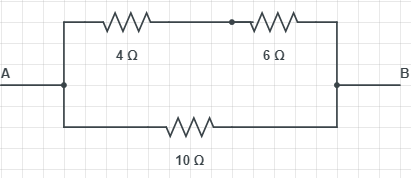
R1=4+6=10ΩR2=10Ω
(Since 4Ω and 6Ω are in series)
Req1=R11+R21
(Since R1 And R2 are in parallel)
Req1=101+101=5Ω1Req=5Ω
Put value in equation (1) we get,
I=55=1A
So, the correct answer is “Option A”.
Note: Meter Bridge works on Wheatstone bridge network’s principle. Meter Bridge is the modification of Wheatstone’s network which is generally used to determine unknown resistance. It is also called Wheatstone's meter bridge. Since the length of wire used in this is one meter, it is called Meter Bridge.
