Question
Question: In the Atwood machine (data as in figure), P is a massless pulley, and springs \[{{S}_{1\text{ }}}\t...
In the Atwood machine (data as in figure), P is a massless pulley, and springs S1 and S2 are also massless. If the blocks are let go, the readings in S1 and S2 will respectively be:
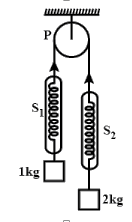
Solution
Here we have to find reading for S1 and S2 where both are the massless spring, when we let go the blocks, it will created a tension in the spring and the rope or the string. As the springs are massless it will only have tension. Therefore we have to find the tension in the spring. We can draw a simple diagram to find the force on the blocks and find the tension.
Complete answer:
We can replace the springs with the rope, as the springs are massless and it is attached between the rope and the block. The tension experienced by the spring will be the same as the tension created in the rope. As there is a single rope therefore the tension will be the same in both the springs. Hence the given diagram can be drawn as
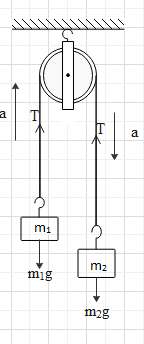
The forces experienced by the block of mass m1 are the upward tension, the downward gravitational pull and the upward force, then the equation for the block m1 is given as
m1g−T=m1a ………….. (i)
Where g is acceleration due to gravity.
The forces experienced by the block m2
are the upward tension, the downward gravitational pull and the downward force, then the equation for the block m2 is given as
T−m2g=m2a………….. (ii)
Adding the both equations we get
