Question

In the arrangement shown, the relation between the acceleration of wedge 1 and wedge 2 is

$\begin{aligned} & {\text{A}}{\text{. }}{a_1} = {a_2}\sin \theta \\\ & {\text{B}}{\text{. }}{a_1} = {a_2}\cos \theta \\\ & {\text{C}}{\text{. }}{a_1} = {a_2}\cot \theta \\\ & {\text{D}}{\text{. }}{a_1} = {a_2}\tan \theta {\text{ }} \\\ \end{aligned}$

Answer 1

In the diagram, we are given the directions of two accelerations and also the angle between the two wedges. Based on the given directions and by using the simple trigonometric relations for sides of the triangle formed by the two accelerations, we shall be able to get the required answer.

Complete step-by-step solution
Consider the given arrangement of two wedges. We are given the directions of two accelerations and also the angle between the two wedges which is equal to $\theta$.

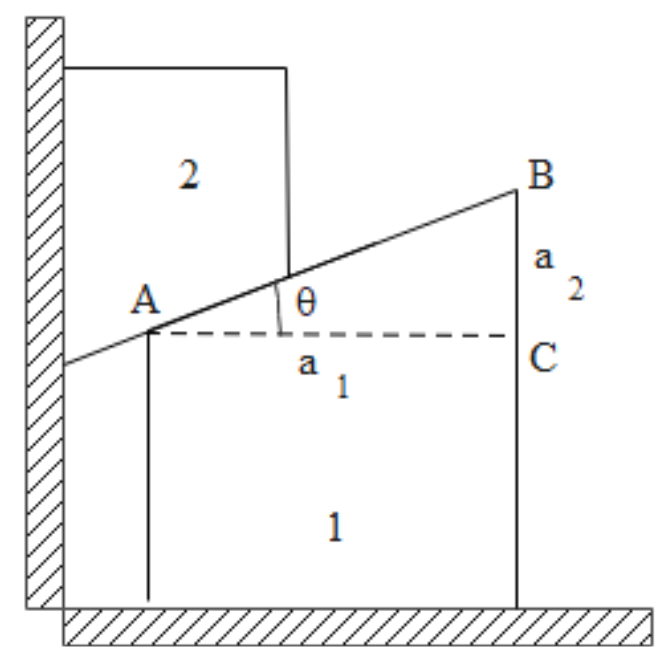
Based on the directions of the two accelerations, we can get a triangle ABC, in which AC is equal to ${a_1}$ while BC is equal to ${a_2}$.
As we know that in a right angled triangle, the ratio of the perpendicular and the base is equal to the tangent of the angle at the base of the triangle. In the same way, in the triangle ABC, we can write the following expression for the two accelerations.
$\dfrac{{BC}}{{AC}} = \tan \theta$
Inserting the known values of sides, we get
$\begin{aligned} &\Rightarrow \dfrac{{{a_2}}}{{{a_1}}} = \tan \theta \\\ &\Rightarrow {a_2} = {a_1}\tan \theta \\\&{\text{or }}{a_1} = {a_2}\cot \theta \\\ \end{aligned}$
This is the required relation between the acceleration of wedge 1 and the acceleration of wedge 2. Therefore, the correct answer is option C.

Note: 1. The two accelerations are vector quantities and their directions have allowed us to construct a triangle from which we could get a relation between them.
2. The obtained expression shows that the two accelerations of the two wedges inclined at an angle to each other are related to each other through the tangent or cotangent of the angle between them. This relation is obtained because the two directions are perpendicular to each other.