Question

In the arrangement shown, the pulleys and the strings are ideal. The acceleration of
block B is

A. $\dfrac{8}{5}$
B. $\dfrac{g}{2}$
C. $\dfrac{{2g}}{5}$
D. $\dfrac{{2g}}{3}$

Answer 1

The given problem is based on Pulleys which work in a load and tension in the string. You need to apply Newton's 2nd law of motion to solve this problem. By using Newton's 2nd law, you can write the equation for both the blocks and solving these equations will give you the answer to this question.
Newton's 2nd law states that the force applied on a body always equal to the multiplication of mass and acceleration .i,e.,
$F = ma$

Complete step by step answer:
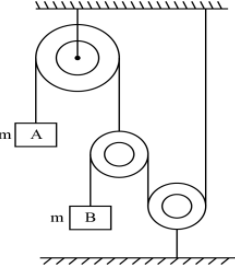
In this question, there are two blocks A and B given, and they are connected with a pulley system, as shown in the figure.

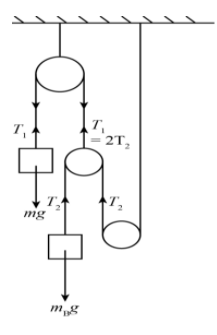
Let us consider that block A is moving up and block B is moving down
The free body diagram of both the masses is shown in the picture.
For block A,

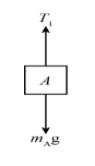
From newton’s 2nd law of motion
${T_1} - {m_A}g = {m_A}{a_1}$ ……………………………(1)
For block B

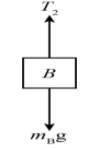
From newton’s 2nd law of motion
${m_B}g - {T_2} = {m_B}{a_2}$ (2)………………………………..(2)
And
${T_1} = 2{T_2}$
By this tension relation, we can say that ${a_2} = 2{a_1}$
Putting the value of ${a_1}$ of in equation 1, we get
${T_1} - {m_A}g = {m_A}\frac{{{a_2}}}{2}$
$2{T_1} - 2{m_A}g = {m_A}{a_2}$…………………………..(3)
Solving 1 and 3
${a_2} = \dfrac{2}{5}g$
Free body diagram plays an important role in these types of pulley problems. Without the free body diagram of the individual mass, we can’t form the equations, and hence solving can be more tricky.
Solving this type of pulley question, sometimes we have to take approximations by just looking at the free body diagram.

So, the correct answer is “Option C”.

Note:
In this case; we took ${a_2} = 2{a_1}$ for solving the equations because we had four unknown quantities and only three equations were there, so with the help of approximations, we can solve pulley questions very easily and quickly. You may go wrong while analyzing motion of the pulleys and the blocks A and B because if you consider the wrong motion, then the equation can't be right hence the final solution gets affected.