Solveeit Logo
Login

Question

Question: In the arrangement shown in the figure, the ends P and Q of an inextensible string move downwards wi...

In the arrangement shown in the figure, the ends P and Q of an inextensible string move downwards with uniform speed u. Pulleys A and B are fixed. The mass m moves upwards with a speed –

& A)\text{ }2u\cos \theta \\\ & B)\text{ }\dfrac{u}{\cos \theta } \\\ & C)\text{ }\dfrac{2u}{\cos \theta } \\\ & D)\text{ }u\cos \theta \\\ \end{aligned}$$
Explanation

Solution

We need to understand the relation between the velocities by which the two pulleys go downwards and the speed with which the body of mass m goes upwards. We have to consider the direction in which the velocities are acting on the mass.

Complete step-by-step answer:
We are given a system of pulleys A and B which are pulled downwards producing a uniform downward motion for both the pulleys. It is also given that the speeds at t=which they move downwards are the same ‘u’. The two pulleys are connected via a rope and a mass hung down at the middle of the system as we can see in the figure.
We need to find the direction of the speeds acting on the mass due to the motion of the two pulleys separately. We know that the mass is connected to the pulley systems by an angle. The speed of the mass has to be related to the speed of the two pulleys through this angle.
We can find the component of velocity which acts against the gravitational force. This component of velocity will be responsible for the upwards movement of the body.

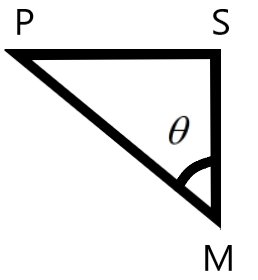
                      ![](https://www.vedantu.com/question-sets/bcda2335-c9b5-4cb3-b4f3-45fcc6f1cf342200541023217404352.png)

Let us consider the motion of the body due to the pulley P alone. We can use the trigonometric relations to find the velocity along the vertical as –

& \text{In }\Delta \text{PMS,} \\\ & \text{cos}\theta =\dfrac{x}{u} \\\ & \therefore x=u\cos \theta \\\ \end{aligned}$$ This is the velocity acting along the vertical. Now, we know that the required velocity is the one acting alone MS, i.e., x. The velocity of the body is therefore, can be given as – $$\therefore x=\dfrac{u}{\cos \theta }$$ **So, the correct answer is “Option B”.** **Note:** The tension on both the ropes on the pulleys P and Q are the same. The velocity of the mass will be the corresponding value which is the resultant of the two speeds. If the velocities of the pulleys are different, then the body tends to have a horizontal component of velocity also.