Question
Question: In the arrangement shown in the figure, pulleys are massless and frictionless and threads are inexte...
In the arrangement shown in the figure, pulleys are massless and frictionless and threads are inextensible, a block of mass m1 will remain at rest, if:
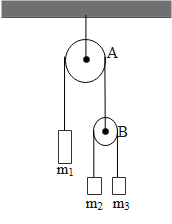
A. m11=m21+m31
B. m1=m2=m3
C. m14=m21+m31
D. m11=m22+m33
Solution
Any object which is in its balance state always has forces acting on it in such a way that the net force on the body becomes zero. The forces acting on a body are represented by the use of a free body diagram. The tension force acting on the FBD is a good way to analyze the forces experienced by a material.
Complete step-by-step answer:
When two objects are moving over a pulley the tension force acting on both the sides of the strings has tension force of the same magnitude.
So the free body diagram of the whole setup mentioned in the question can be given as,
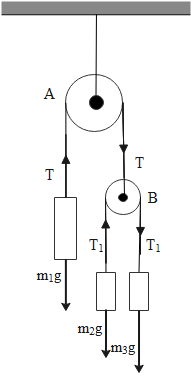
When the mass m1 is at rest the tension force T is equivalent to the downward force m1g.
Mathematically,
m1g=T......(1)
The tension forces T1 along the pulley B will be equal both the side and the sum of these forces is equivalent to the tension force T.
T1=T1
T=T1+T1⇒T=2T1
Let us assume that the mass m3 is pulled to move downward and automatically the mass m2 move upward.
So the force balanced equation of both the masses m2 and m3 will be,
m3(g+a)=T1.........(2)m2(g−a)=T1.........(3)
So by equating equations (1) and (2),
m3(g−a)−m2(g+a)=0⇒m3g−m3a−m2g−m2a=0⇒(m3−m2)g−(m3+m2)a=0⇒a=m3+m2m3−m2×g
So the tension T1 is given as,
T1=m2+m32m2m3g
As a result, the value of tension Twill be,
T=2T1⇒T=m2+m34m2m3g......(4)
From equation (1) and (4) we get that:
m1g=m2+m34m2m3g∴m14=m21+m31
So, when we give a glance over the options mentioned in the question the correct option which satisfies the question is option C.
So, the correct answer is “Option C”.
Note: Pulley is a ring-like structure that can roll easily. Their main function is to reduce friction and increase mobility. These are used in mechanical assemblies where we have to move a certain object using strings or ropes. They work on the principle of surface contact as the surface contact will be less and the friction applied to the body will also be very small.
