Question

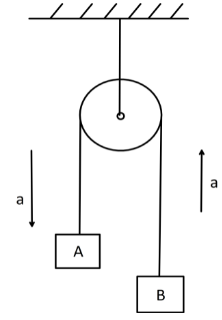
In the arrangement shown in the figure ${M_a}$ and ${M_b}$ are $2\,kg$ and $1\,kg$ respectively. Find the acceleration of the centre of mass of both the blocks.

Answer 1

Any object which is in a balance state always has force acting on it in such a way that the net force on the body becomes zero. The force acting on the bodies will be equal in both the sides when suspended by a pulley. Neglecting friction will lead to simply equating forces on both sides.

Complete step by step answer:
The above question is about the arrangement of pulleys. When two objects are moving over a pulley the tension force acting on both the sides of the string has a tension force of the same magnitude. We neglect the mass of sting attached and the force of friction. Also we ignore any other disturbing forces considering that no external forces. Here Given that,
Mass of object a is ${M_a} = 2Kg$
Mass of the object is..
Acceleration due to gravity is $g$
Now, as ${M_a} > {M_b}$ so acceleration of $A$ is downward and $B$ is upward. For downward assume acceleration is positive and for upward acceleration negative. i.e.,$a(A) = a$ and $a(B) = - a$
here,$\left( {{M_a} + {M_b}} \right)a = \left( {{M_a} - {M_b}} \right)g$
$\Rightarrow \left( {2 + 1} \right)a = \left( {2 - 1} \right)g$
Which gives,
$\Rightarrow a = \dfrac{g}{3}$
Hence Acceleration of body $A$ is ${a_a} = \dfrac{g}{3}$ and acceleration of body $B$ is ${a_b} = -\dfrac{g}{3}$ as it is in the opposite direction.

Thus, Acceleration of centre of mass of both the blocks
${a_{cm}} = \dfrac{{{M_a}{a_a} + {M_b}{a_b}}}{{{M_a} + {M_b}}}$
Putting values we get,
$\Rightarrow {a_{cm}} = \dfrac{{2\left( {g/3} \right) + 1\left( { - g/3} \right)}}{{2 + 1}}$
That is,
$\therefore {a_{cm}} = g/9$ Downward (As it is positive)

Note: Pulley is ring like structure and its main function is to reduce friction and increase mobility. They are used in mechanical assemblies where certain heavy objects are to be moved. Similar questions might be asked just by changing the magnitude of the masses and number of objects attached to any side.