Question
Question: In the arrangement shown in the figure. If the block is moving horizontally with speed \(10{\text{ }...
In the arrangement shown in the figure. If the block is moving horizontally with speed 10 m/s, then find the speed of the hanging block at a given instant of time.
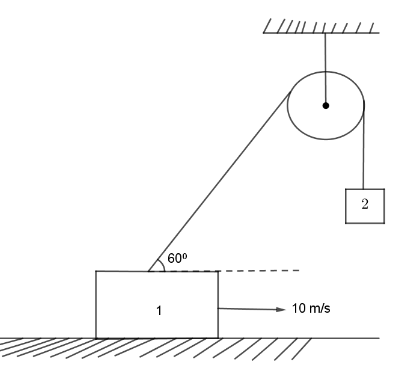
Solution
We will first perform an intuitive analysis of the given situation and try to mentally stimulate what would happen. Then, we will mathematically depict our intuition. We will use the concept of rectangular components. Then, finally, we will evaluate the actual numerical value.
Complete step by step answer:
Here, we can clearly see that the mass 1 moves horizontally forcing the string to pull the mass 2 upwards. Now, as the mass and the string makes an angle of 60o between them, we can safely say that the velocity vector will also make an angle of 60o with the string.
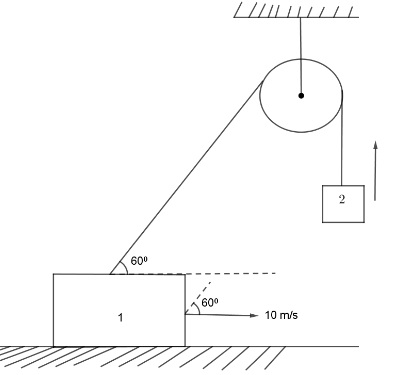
Now, from our knowledge of the situation, we can say that the component of the velocity of the mass 1 in the direction of the string will be responsible for pulling the mass 2 upwards. Thus, we can say that the velocity with which the string is being stretched will be the velocity of the mass 2.
Thus, the velocity of the mass 2 is,
10 cos60o
Now, substituting cos60o = 21, we get
The velocity of the mass 2 is,
10 × 21 = 5
Thus, the mass 2 will move upwards with a velocity of 5 m/s.
Additional Information:
Rectangular components of a vector can be defined as the value or the magnitude of involvement of two mutually perpendicular directions on the actual vector.
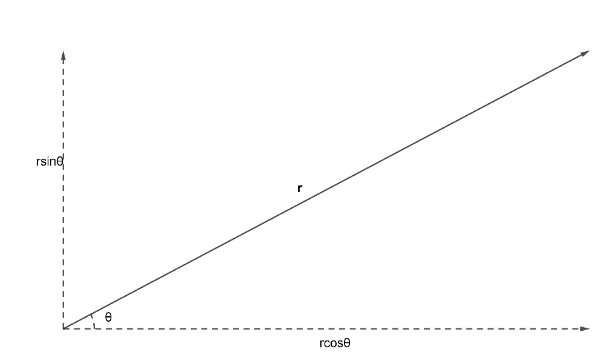
Here, r is the actual vector making an angle θ with the horizontal. Now, if we want to evaluate the magnitude of contribution of the horizontal and the vertical directions individually, we simply use our idea of basic trigonometric ratios.Thus, we can say the magnitude of contribution of the horizontal direction can be written as r cosθ. And the vertical direction by r sinθ.
These components of the actual vector in two mutually perpendicular directions are known as rectangular components. From the example we can say that the net result of r cosθ in the horizontal and r sinθ in the vertical is same as a vector r making an angle θ with the horizontal. This is the physical significance or we can say the geometrical interpretation of rectangular components.
Note: Students should remember that these types of problems should be solved taking the assumption that the pulley and the string involved are frictionless and massless.Students often commit mistakes in evaluating the trigonometric value of the given angle. Students also should be cautious while taking the components of a targeted vector as they should carefully see the angle formed by the vector with a particular direction.
