Question
Question: In the arrangement shown in figure when the switch \( {S_2} \) is open, the galvanometer shows no de...
In the arrangement shown in figure when the switch S2 is open, the galvanometer shows no deflection for l=2L . When the switch S2 is closed, the galvanometer shows no deflection for 125L . The internal resistance (r) of 6V cell and the emf E of the other battery respectively are
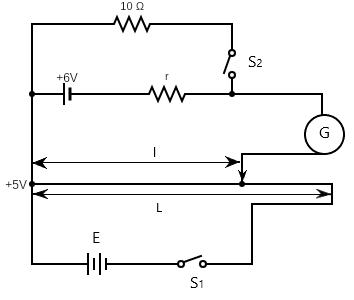
(A) 3Ω,8V
(B) 2Ω,12V
(C) 2Ω,24V
(D) 3Ω,12V
Solution
When galvanometer shows no deflection, it means no current is flowing through it. In this case the ratio of voltage across the wire to the point where the jockey is to the voltage across the entire wire is equal to the ratio of the length to the jockey is to the ratio of the entire length of the potentiometer.
Formula used: In this solution we will be using the following formulae;
E2E1=L2L1 where E1 is the voltage across the potentiometer to where the jockey is, E2 is the voltage across the entire potentiometer, L1 is the length of the wire of the potentiometer to where the jockey is, and L2 is the length of the entire wire.
Complete step by step answer:
When the switch S2 is closed, no current will flow through the section of the circuit. Now at the same time, no deflection in the galvanometer if the jockey is at l=2L . At this point, we can use the equation
E2E1=L2L1 where E1 is the voltage across the potentiometer to where the jockey is, E2 is the voltage across the entire potentiometer, L1 is the length of the wire of the potentiometer to where the jockey is, and L2 is the length of the entire wire. Hence,
E6=L2L
Simplifying, and calculating for E , we have
E=12V .
Also, there is no deflection when the switch S2 is closed at l=125L , however current will flow through the upper branch of the circuit.
Applying kirchoff’s rule to that circuit, we have
6−Ir−10I=0
⇒I=r+106
Hence, the voltage from the cell to beyond the internal resistance is
V=6−Ir=6−r+106r
Now, because there’s no deflection in galvanometer, we have
EV=L125L . replacing E with 12 volts and finding V , we have that
V=5V
Hence,
6−r+106r=5
⇒r+106r=1
Solving for r , we have
r=2Ω
Hence, the correct option is B.
Note:
For clarity, observe that the internal resistance does not affect the emf of the 6 V cell in the first case but is affected in the second case. This is because in the first case, current is not flowing through the cell, thus the internal resistance is dormant.
