Question
Question: In the arrangement shown in figure, pulleys are mass less and frictionless and threads are inextensi...
In the arrangement shown in figure, pulleys are mass less and frictionless and threads are inextensible. Block of mass m1 will remain at rest:
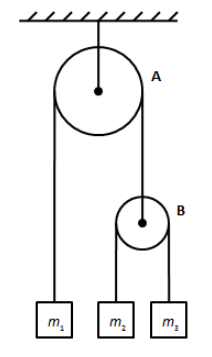
A. m11=m21+m31
B. m14=m21+m31
C. m1=m2+m3
D. m11=m22+m33
Solution
For the block of mass m1 to be at rest, the acceleration of this block must be zero. Assume that one of the two blocks connected to pulley B move downwards and apply Newton’s second law for both the blocks. Solve the equations simultaneously to get the required expression.
Formula used:
Newton’s second law, Fnet=ma,
where, m is the mass and a is the acceleration.
Complete Step by Step Answer:
For the block of mass m1 to be at rest, the acceleration of this block must be zero. Let the tension in the thread connected to m1 is T and also the tension in the thread connected to m2 and m3 is T1. We assume the block m2 and m3 do not stay at rest and the block m2 move downward with acceleration a.
Thus, the block m3 will move upward with the same acceleration. Let us draw the free body diagram of the forces acting on the blocks as follows,

From the above figure, we can write,
T=m1g …… (1)
Also, 2T1=T
⇒T1=2T …… (2)
Applying Newton’s second law of motion on m2, we can write,
T1−m2g=−m2a
⇒m2g−T1=m2a …… (3)
Applying Newton’s second law of motion on m3, we can write,
T1−m3g=m3a …… (4)
Adding equation (3) and (4), we get,
m2g−m3g=(m2+m3)a
⇒a=(m2+m3m2−m3)g
Substituting the value of a in equation (4), we get,
T1−m3g=m3(m2+m3m2−m3)g
⇒T1=m3(m2+m3m2−m3)g+m3g
⇒T1=m3g(m2+m3m2−m3+1)
⇒T1=m3g(m2+m3m2−m3+m2+m3)
⇒T1=m3g(m2+m32m2)
⇒T1=(m2+m32m2m3)g
Substituting T1=2T from equation (2) in the above equation, we get,
2T=(m2+m32m2m3)g
⇒T=(m2+m34m2m3)g
Substituting T=m1g from equation (1) in the above equation, we get,
m1g=(m2+m34m2m3)g
⇒m1=(m2+m34m2m3)
⇒m2+m3=m14m2m3
⇒m2m3m2+m2m3m3=m14
⇒m31+m21=m14
∴m14=m21+m31
So, the correct answer is option B.
Note: The direction of tension should always be towards the rigid support and the direction of weight should be towards the ground irrespective of the inclination. For the first block to do not move, both pulleys A and B also should not move. If the direction of the acceleration is downwards, the force also has the direction of acceleration according to Newton’s second law of motion.
