Question

In the arrangement shown in figure, $\mu_1=0.1$, $\mu_2=0.4$, $M=20$ kg

Find the maximum value of $m$ for which the arrangement can be in equilibrium.

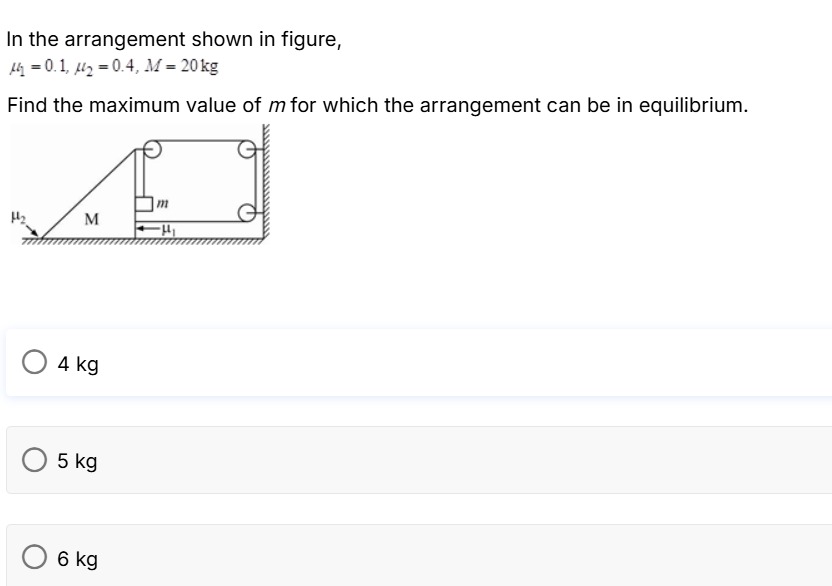
• A. 4 kg
• B. 5 kg
• C. 6 kg

Answer 1

Answer: (A)

4 kg

Answer 2

To find the maximum value of 'm' for which the arrangement can be in equilibrium, we need to analyze the forces acting on block M and block m.

1. Identify forces on block 'm': The tension in the string T equals the weight of 'm', so $T = mg$.

2. Analyze the pulley system: The string passes over two pulleys attached to block M. When block M moves horizontally by a distance $x$, the total length of the string pulled by 'm' is $2x$. This implies that the effective horizontal force exerted by the string on block M is $2T$. This force acts to the right, tending to move M to the right.

3. Identify forces on block M:

   • Weight $Mg$ (down).
   • Normal force from ground $N_1$ (up).
   • Normal force from inclined wall $N_2$ (perpendicular to wall, $45^\circ$ to horizontal, pointing left-up).
   • Friction from ground $f_1 = \mu_1 N_1$ (left, opposing motion).
   • Friction from inclined wall $f_2 = \mu_2 N_2$ (along incline, up the incline, opposing relative motion).

4. Resolve forces on M into components and apply equilibrium conditions (ΣFx = 0, ΣFy = 0):

   • Assuming M tends to move right, $f_1$ acts left. The relative motion of M against the inclined wall is downwards along the incline, so $f_2$ acts upwards along the incline.

   • $N_2$ has components $N_2 \cos 45^\circ$ (left) and $N_2 \sin 45^\circ$ (up).

   • $f_2$ has components $f_2 \sin 45^\circ$ (right) and $f_2 \cos 45^\circ$ (up).

   • Vertical Equilibrium (ΣFy = 0): $N_1 + N_2 \sin 45^\circ + f_2 \cos 45^\circ - Mg = 0$. Substitute $f_2 = \mu_2 N_2$ and $\sin 45^\circ = \cos 45^\circ = 1/\sqrt{2}$:

     $N_1 = Mg - N_2 (1 + \mu_2)/\sqrt{2}$ (Equation 1)

   • Horizontal Equilibrium (ΣFx = 0): $2T - N_2 \cos 45^\circ + f_2 \sin 45^\circ - f_1 = 0$. Substitute $f_1 = \mu_1 N_1$, $f_2 = \mu_2 N_2$:

     $2T = N_2 (1 - \mu_2)/\sqrt{2} + \mu_1 N_1$ (Equation 2)

5. Solve the system of equations: Substitute Equation 1 into Equation 2 and solve for $T$ (or $m$) in terms of $N_2$, or vice versa.

   $2T = N_2 (1 - \mu_2)/\sqrt{2} + \mu_1 [Mg - N_2 (1 + \mu_2)/\sqrt{2}]$

   $2T - \mu_1 Mg = \frac{N_2}{\sqrt{2}} [(1 - \mu_2) - \mu_1 (1 + \mu_2)]$

   $2T - \mu_1 Mg = \frac{N_2}{\sqrt{2}} [1 - \mu_1 - \mu_2 (1 + \mu_1)]$

6. Apply conditions for normal forces: For equilibrium, normal forces must be non-negative ($N_1 \ge 0$ and $N_2 \ge 0$). This gives the limiting conditions for 'm'.

   • From $2T - \mu_1 Mg = \frac{N_2}{\sqrt{2}} [1 - \mu_1 - \mu_2 (1 + \mu_1)]$, since $N_2 \ge 0$ and the term in brackets is positive ($1 - 0.1 - 0.4(1.1) = 0.9 - 0.44 = 0.46 > 0$), we must have $2T - \mu_1 Mg \ge 0$.

     $2mg - \mu_1 Mg \ge 0 \implies 2m \ge \mu_1 M \implies m \ge \frac{0.1 \times 20}{2} = 1$ kg.

   • From $N_1 = Mg - N_2 (1 + \mu_2)/\sqrt{2}$, for $N_1 \ge 0$, we must have $Mg \ge N_2 (1 + \mu_2)/\sqrt{2}$.

     Substitute $N_2 = \frac{2\sqrt{2}(m-1)g}{0.46}$ (derived from the horizontal equilibrium equation):

     $Mg \ge \frac{2\sqrt{2}(m-1)g}{0.46} \frac{(1+\mu_2)}{\sqrt{2}}$

     $M \ge \frac{2(m-1)(1+\mu_2)}{0.46}$

     $20 \ge \frac{2(m-1)(1+0.4)}{0.46}$

     $20 \ge \frac{2(m-1)(1.4)}{0.46}$

     $20 \times 0.46 \ge 2.8 (m-1)$

     $9.2 \ge 2.8 (m-1)$

     $m-1 \le \frac{9.2}{2.8} = \frac{92}{28} = \frac{23}{7}$

     $m \le 1 + \frac{23}{7} = \frac{7+23}{7} = \frac{30}{7}$ kg.

7. Determine the maximum 'm': The maximum value of 'm' for equilibrium is $30/7 \approx 4.2857$ kg. Among the given options (4 kg, 5 kg, 6 kg), the largest value that is less than or equal to $30/7$ kg is 4 kg.