Question

in the arrangement shown in figure, ${m_1} = 1kg$ and ${m_2} = 2kg$. Pulley is massless and strings are light. For what value of $M$ the mass ${m_{}}$ moves with constant velocity? (Neglect friction)

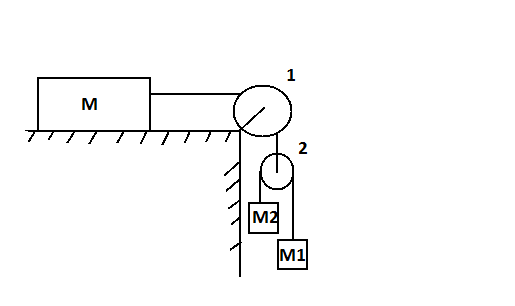
A) $6kg$
B) $4kg$
C) $8kg$
D) $10kgs$

Answer 1

As block of mass ${m_1}$ has to move with constant acceleration, the net acceleration of ${m_1}$ will be equal to $0$. This will give the relation between the relative acceleration and systemic acceleration. The net acceleration of mass ${m_2}$ is balanced by the resultant of weight and tensional force. This further given an equation from which the systemic acceleration can be calculated.
Tensional force in mass ${m_1}$ balances s weight. We will be able to determine the tensional force of the strings from this. The tension in the string of mass $M$ balances its horizontal pull under acceleration and we will be able to determine the force acting upon $M$. These two equations will help us to finally determine the mass of block $M$.

Formulae used: Net acceleration of block ${m_1}$ $:a' - a$.
Where $a'$ is the relative acceleration of the system of blocks ${m_1}$ & ${m_2}$ and $a$ is the acceleration of the entire system meaning it is too of the pulleys and mass $M$. Both of them are expressed in meter per second square $(m/{s^2})$.
Resultant of tensional force and weight of block ${m_1}$ $:T - {m_1}g$.
Where $T$ is the tension developed in the string of the system and is expressed in Newton $(N)$, ${m_1}$ is the mass of $1kg$ block and $g$ is the acceleration due to gravity and is assumed to be $9.8m/{s^2}$.
Balancing force of tension in horizontal string of pulley $1$ and weight of block of mass $M$ $:2T = Ma$
Where $T$ is the tension developed in the string of the system and is expressed in Newton $(N)$ and $M$ is the mass of the horizontal block and is expressed in kilograms $(kg)$.
Resultant of tensional force of weight of block ${m_2}$ $:{m_2}g - T = a + a'$.
Where $T$ is the tension developed in the string of the system and is expressed in Newton $(N)$, ${m_2}$ is the mass of $2kg$ block and $g$ is the acceleration due to gravity and is assumed to be $9.8m/{s^2}$.

Complete step by step solution:

Acceleration in the body having mass $M$ is equal to the acceleration in pulleys $1$ and $2$. But the blocks of mass ${m_1}$ and ${m_2}$, having different masses, have different amounts of velocity. Nonetheless, the velocity is conserved in the given system, that is, velocity everywhere will be the same.
There is an added component of relative velocity in ${m_1}$ and ${m_2}$. ${m_2}$ being heavier $(2kg)$ is pulled downward due to gravitational pull with and a net acceleration of $a' + a$ and ${m_1}$ moves upward with a net acceleration of $a' - a$.
As ${m_1}$ move with constant acceleration,
$a' - a = 0 \\\ \Rightarrow a' = a \\\$
Also, tension in the strings balances the weight of the blocks and the only force under which the system is gravity.
Therefore for mass ${m_1}$,
$T - {m_1}g = 0 \\\ \Rightarrow T = {m_1}g = 1 \times 9.8 \\\ \Rightarrow T = 9.8N \\\$
Due to its horizontal alignment, the only pulling force acting on mass $M$ is the systemic acceleration and it is equal to the tension in the strings connecting it to pulley $1$.
$2T = Mg$
Substituting value of $T$ we get,
$Ma = 2 \times 9.8$
$\Rightarrow Ma = 19.6N$
We know for ${m_2}$,
${m_2}g - T = a + a'$
But we found that $a' = a$.
Substituting everything we get,
$2a = (2 \times 9.8) - 9.8 \\\ \Rightarrow a = \dfrac{{9.8}}{2} = 4.9m/{s^2} \\\$
Finally we can finally calculate the value of $M$.
Substituting the value of $a$ we get,
$Ma = 19.6 \\\ \Rightarrow M = \dfrac{{19.6}}{{4.9}} \\\ \Rightarrow M = 4kg \\\$

Therefore, for a value of $4kg$ for $M$ the mass ${m_1}$ moves with constant velocity.

Additional information: Pulley systems make the lifting of loads easier. The more pulleys in a system, the lesser the manual labor required.

Note: It is important to note the mass of each block. The one with greater mass will move downwards and the lighter one will be pulled upwards. It does not depend on the initial arrangement of the system.