Question

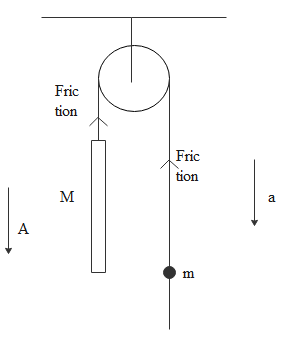
In the arrangement shown in figure above the mass of the rod M exceeds the mass m of the ball. The ball has an opening permitting it to slide along the thread with some friction. The mass of the pulley and the friction in its axle are negligible. At the initial moment the ball was located opposite the lower end of the rod. When set free, both bodies began moving with constant accelerations. The rod length equals l. The friction force between the ball and the thread if t seconds after the beginning of motion the ball got opposite the upper end of the rod is ${F_{fr}} = \dfrac{{xlmM}}{{(M - m){t^2}}}$​. Find x.

Answer 1

Let us assume a condition where m is not fixed to string and there is no friction at all between the string and mass m. Then m will fall freely and M also will fall freely. Since there is friction between m and string these are not falling down freely. Now this friction force is responsible for the tension in the string. So tension will be nothing but friction force.

Formula used:
${s_{relative}} = \dfrac{1}{2}{a_{relative}}{t^2}$

Complete answer:
we observe with respect to small mass m. It is given that M>>m. Hence M will be moving in downward direction due to its weight and m will be moving in downward direction due to gravity. Let acceleration of m is a. While acceleration of M be A. acceleration of M with respect to m will be A – a. It is given that m reached top of M in time t. Distance travelled is length of M which is l. Now we apply kinematic equation

${s_{relative}} = \dfrac{1}{2}{a_{relative}}{t^2}$
${s_{relative}}$ = l
${a_{relative}}$ = A - a
So from formula we get $l = \dfrac{1}{2}(A - a){t^2}$ …eq 1
Weight of m is mg whereas weight of M is Mg
Tension is nothing but frictional force let friction be f
By balancing the forces at mass m and mass M we get
mg – f = ma …eq 2
Mg – f = MA …eq 3
Now if we multiply equation 3 with m we get
Mmg – fm = MmA … eq 4
Now if we multiply equation 2 with M we get
Mmg - fM = mMa …eq 5
By Subtracting equation 5 from equation 4 then we get
$f = \dfrac{{mM(A - a)}}{{M - m}}$ … eq 6
From equation 1 we have $(A - a) = \dfrac{{2l}}{{{t^2}}}$
By substituting above result in equation 6 we get
$f = \dfrac{{2mMl}}{{(M - m){t^2}}}$

So the value of x will be 2.

Note:
Here we are considering both accelerations downward because both masses are mainly affected by gravity rather than by frictional force. we consider motion of M relative to m because with respect to ground their motions will be different and considering with respect to ground makes the problem hard.