Question
Question: In the arrangement shown given that a biconvex lens of radius of curvature equal to \(10cm\) and a c...
In the arrangement shown given that a biconvex lens of radius of curvature equal to 10cm and a concave mirror has focal length equal to 20cm. Then find the distance x such that the final image formed by the system coincides with the object.
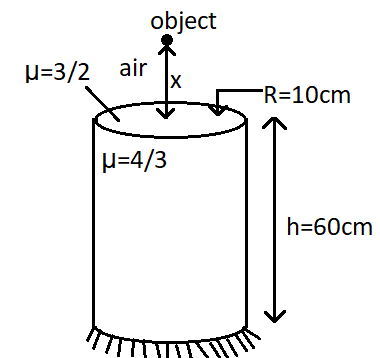
Solution
Using the formula for the focal length of the lens in the terms of the object and the image distance, we can find the object distance. Here the image distance will be the difference of the distance of the lens and the mirror and the focal length of the mirror.
Formula used: In this solution we will be using the following formula,
⇒f1=u1+v1
where f is the focal length of the lens, u is the object distance and v is the image distance.
Complete step by step solution:
In the problem, we are given that the focal length of the lens is 10cm as for a biconvex lens, the radius of curvature is the focal length. Now the image distance of the combination will be the difference between the distance between the lens and the mirror and the focal length of the mirror.
So can use the formula for the lens given as,
⇒f1=u1+v1
Here, f=10cm and v=60−20
So the image distance is v=40cn
Now sub substituting the values we get,
⇒101=u1+401
So taking the u1 to the LHS we get,
⇒u1=101−401
Taking LCM as 40,
⇒u1=104−1
On taking the inverse we get,
⇒u=310cm
hence the object distance is u=3.33cm.
Note:
A biconvex lens is a simple lens consisting of two convex surfaces which generally have the same radius of curvature. A concave mirror is a portion of a hollow sphere where the outer surface of the sphere is painted so that the inner surface reflects the light falling on it.
