Question
Question: In the arrangement shown a solid cylinder of mass \(M\) and radius \(R\) is suspended with the help ...
In the arrangement shown a solid cylinder of mass M and radius R is suspended with the help of an ideal string, and the lift is moving upward with acceleration g/3. The tension in the string is
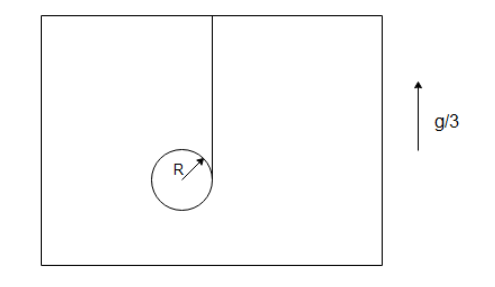
A) 125mg
B) 34mg
C) 43mg
D) 94mg
Solution
The tension in the string can be determined from the force balance of the string. It can also be determined from the angular motion of the solid cylinder on the string. We will equate these two equations to determine the tension in the string.
Formula used: In this solution, we will use the following formulae:
Torque on the cylinder: τ=F.R=I.α where F is the force or the tension in the string, R is the radius of the pulley, I is the moment of inertia of the rod, and α is the angular acceleration of the cylinder.
Complete step by step answer:
Let us start by drawing a free body diagram of the situation described:
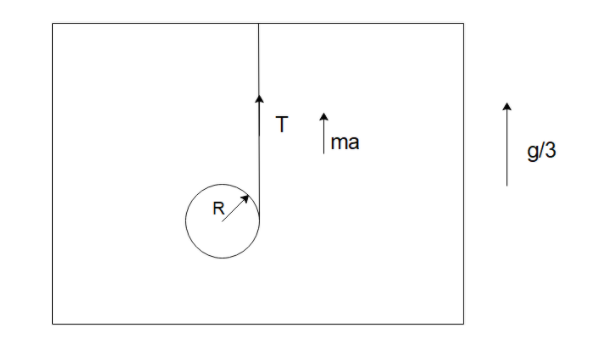
We can see that the net acceleration experienced by the system will be due to gravity and the acceleration of the lift as a=g+3g=34g.
Then the force balance of the diagram in the vertical direction will be
34mg−T=ma
where a is the net acceleration of the object.
Now looking at the angular motion of the cylinder, we know that the moment of inertia of a solid cylinder is calculated as 2mR2. Then the torque acting on the cylinder due to the unrolling of the string will be
TR=2MR2α
As the angular acceleration is the product of the linear acceleration and the radius of the sphere, we have α=aR. Then the above equation can be written as
ma=2T
Equating equation (1) and (2), we get
34mg−T=2T
Which gives us the tension as
T=94mg which corresponds to option (D).
Note: Such questions always require knowledge of the translational dynamics as well as the rotational dynamics of the object. We should also know the moment of inertia of certain objects like cylinders about different axes as these objects are frequently encountered in such questions.
