Question
Question: In the arrangement of resistances shown in the figure, the potential difference between \(B\) and \(...
In the arrangement of resistances shown in the figure, the potential difference between B and D will be zero when the unknown resistance X is
A. 4 Ω
B. 2 Ω
C. 3 Ω
D. 6 Ω
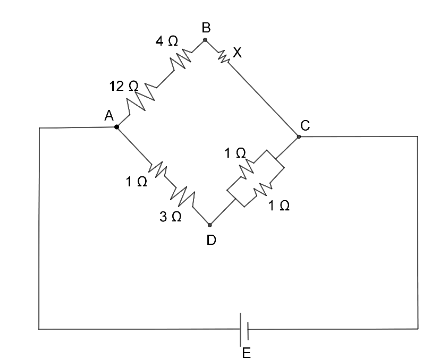
Solution
We will use the concept of wheatstone bridge principle. Then, we will apply the principle in the given circuit. Finally we will evaluate the numerical value of the unknown resistance.
Formulae used:
RSeries = R1 + R2 + .... + Rn
⇒RParallel1 = R11 + R21 + ... + Rn1
⇒R2R1 = R4R3
⇒I = RV
Complete step by step answer:
Here, we are given a few resistors.
Let, R1 = 12 Ω
R2 = 4 Ω
⇒R3 = X Ω
⇒R4 = 1 Ω
⇒R5 = 1 Ω
⇒R6 = 3 Ω
⇒R7 = 1 Ω
Now, clearly R4 and R5 are parallel to each other. Thus, resistance across CD is,
RCD1 = R41 + R51
Substituting the values, we get
RCD = 0.5 Ω
Again, resistance across AB is,
RAB = R1 + R2
Substituting the values, we get
RAB = 16 Ω
Again, resistance across BC,
RBC = R3
Substituting the value, we get
RBC = X Ω
Also, resistance across AD,
RAD = R6 + R7
Substituting the values, we get
RAD = 4 Ω
Now, for the potential difference across BD to be zero, the ratio of the resistances across the arms of the two sides should be equal. This is known as the wheatstone bridge principle.The equation of the same is,
RADRAB = RCDRBC
Substituting the values, we get
416 = 0.5X
Further, we get
X = 0.5 × 416
After further calculation, we get
∴X = 2 Ω
Hence, the correct option is B.
Note: Students should remember that the wheatstone bridge principle is applicable for parallel positions. Thus, they should firstly very carefully observe the given circuit.Students often make mistakes while judging the type of connection (parallel or circuit). This makes them wrongly evaluate the net resistance. This will further make them not arrive at the correct answer. Students should keep the actual idea behind this method as that the potential difference between two points is zero only when their potentials are equal. Thus, for them to be equal the arms on either sides of the points are proportional as this will make same amount of current flowing through each will be the same
