Question

In the arrangement as shown, the tension ${{\text{T}}_{\text{2}}}$ is , (Take $g=10\text{ m/}{{\text{s}}^{2}}$)

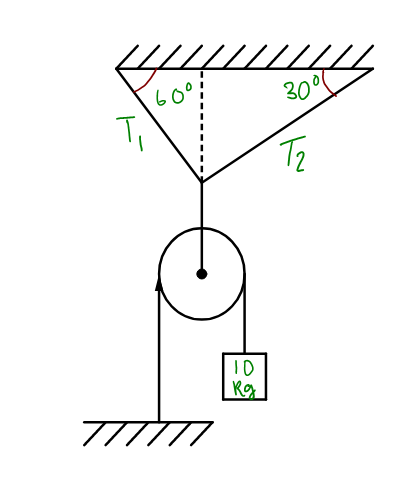
A. 50 N
B. 100 N
C. $50\sqrt{3}\text{ N}$
D. $100\sqrt{3}\text{ N}$

Answer 1

Hint: There will be a tension in the string acting opposite to the weight. The tension can split into two smaller tensions ${{\text{T}}_{1}}\text{ and }{{\text{T}}_{2}}$ by connecting the main string to two other strings which are on a fixed surface.

Complete step by step answer:

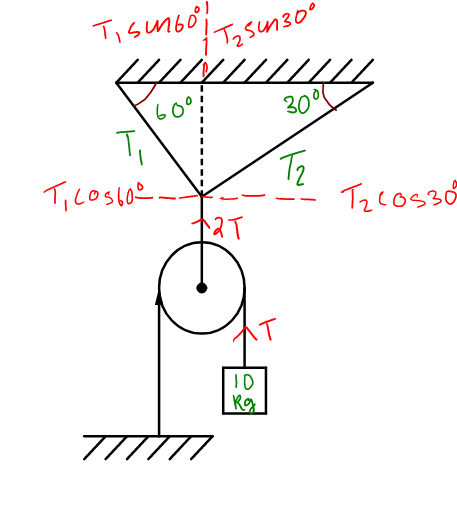
The weight of the mass m acting downwards is given by the formula,
$\text{W}=\text{mg}$
Here, m=10kg, $g=10\text{ m/}{{\text{s}}^{2}}$
$\therefore \text{ W}=100\text{N}$ ….. equation (1)
The weight acting will be equal to the tension in the string.
$\therefore \text{ T=W=100N}$
The tension or force on the string of the pulley will be 2T.
Splitting ${{\text{T}}_{1}}\text{ and }{{\text{T}}_{2}}$ into horizontal and vertical components as shown in the figure, we can write the forces acting along the x axis as,
$\begin{aligned} & {{T}_{1}}\cos {{60}^{\circ }}={{T}_{2}}\cos {{30}^{\circ }} \\\ & \Rightarrow {{T}_{1}}\left( \dfrac{1}{2} \right)={{T}_{2}}\left( \dfrac{\sqrt{3}}{2} \right) \\\ \end{aligned}$
$\therefore {{\text{T}}_{\text{1}}}={{\text{T}}_{\text{2}}}\sqrt{\text{3}}$ ….equation (1)
Forces along the horizontal direction is given by,
${{T}_{1}}\sin {{60}^{\circ }}+{{T}_{2}}\sin {{30}^{\circ }}=2T$
$\begin{aligned} & \Rightarrow {{T}_{1}}\sin {{60}^{\circ }}+{{T}_{2}}\sin {{30}^{\circ }}=200\text{N} \\\ & \Rightarrow {{T}_{1}}\left( \dfrac{\sqrt{3}}{2} \right)+{{T}_{2}}\left( \dfrac{1}{2} \right)=200\text{N} \\\ \end{aligned}$
From equation (1) we can substitute $T_1$ in the above equation.
$\begin{aligned} & {{T}_{2}}\sqrt{3}\left( \dfrac{\sqrt{3}}{2} \right)={{T}_{2}}\left( \dfrac{1}{2} \right)=200 \\\ & \Rightarrow 4{{T}_{2}}=400 \\\ \end{aligned}$
$\therefore {{\text{T}}_{\text{2}}}=100\text{N}$
So the answer to the question option (B) 100 N

Additional Information:
Pulley systems are used to provide us with a mechanical advantage, where the amount of input effort is multiplied to exert greater forces on a load.
They are typically used for hauling and lifting loads but can also be used to apply tension within a system such as in a Tensioned Line or Tyrolean.
We can see pulley through all the ages. Pulley was extensively used by people in the past to lift heavy loads and it was seen in the works of early mathematicians like Archimedes.

Note: The tension ${{\text{T}}_{\text{1}}}$ has the value $100\sqrt{3}\text{ N}$.
The same problem can be solved using Lami’s theorem.