Question

In the angle of elevation of a cloud from a point P which is 25m above a lake be ${30^ \circ }$ and the angle of depression of reflection of the cloud in the lake from P be ${60^ \circ }$ , then the height of cloud (in meter) from the surface of the lake is?
A. 42
B. 50
C. 45
D. 60

Answer 1

Start by assuming the height of the cloud as some variable from the surface of the lake. Draw the diagram accordingly and take the triangle which involves clouds directly and apply the required trigonometric formula of $\tan \theta = \dfrac{{perpendicular}}{{base}}$, obtain the base value . Similarly take another triangle which involves reflection of clouds and apply the same formula. Solve the two relations formed and find the value of height.

Complete step-by-step answer:

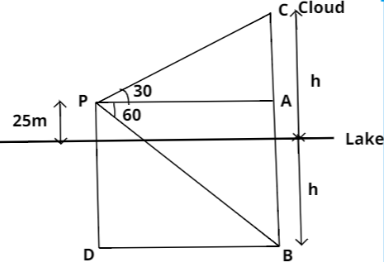
As we can see in the figure, Point C represents cloud and point B its reflection so both the points are equal distance from the surface of the lake.
Now , Let the height of the cloud be h from the surface of the lake
Now, In $\Delta PAC$

$\tan {30^ \circ } = \dfrac{{AC}}{{AP}}$
And from the figure, we can see AC = h – 25
$\tan {30^ \circ } = \dfrac{{h - 25}}{{AP}} = \dfrac{1}{{\sqrt 3 }}$
$\Rightarrow AP = \sqrt 3 \left( {h - 25} \right) \to eqn.1$
Now, In $\Delta PBD$

$\angle APB = \angle PBD = {60^ \circ }({\text{Alternate angle)}}$
$\tan {60^ \circ } = \dfrac{{PD}}{{BD}}$
We can easily see PABD is a rectangle so
AP = BD
$\tan {60^ \circ } = \dfrac{{PD}}{{AP}}$
From the figure we can see PD = h+25
$\tan {60^ \circ } = \dfrac{{h + 25}}{{AP}} = \sqrt 3 \\\ AP = \dfrac{{h + 25}}{{\sqrt 3 }} \to eqn.1 \\\$
From equation(1) and equation(2) , we get
$\sqrt 3 \left( {h - 25} \right) = \dfrac{{h + 25}}{{\sqrt 3 }} \\\ \Rightarrow 3\left( {h + 25} \right) = h + 25 \\\ \Rightarrow 3h + 75 = h + 25 \\\ \Rightarrow 2h = 100 \\\ \Rightarrow h = 50m \\\$
Therefore , the height of the cloud is 50 m from the water surface.

So, the correct answer is “Option B”.

Note: As we can see in the figure, Point C represents cloud and point B its reflection so both the points are equal distance from the surface of the lake.
Now , Let the height of the cloud be h from the surface of the lake
Now, In $\Delta PAC$

$\tan {30^ \circ } = \dfrac{{AC}}{{AP}}$
And from the figure, we can see AC = h – 25
$\tan {30^ \circ } = \dfrac{{h - 25}}{{AP}} = \dfrac{1}{{\sqrt 3 }}$
$\Rightarrow AP = \sqrt 3 \left( {h - 25} \right) \to eqn.1$
Now, In $\Delta PBD$

$\angle APB = \angle PBD = {60^ \circ }({\text{Alternate angle)}}$
$\tan {60^ \circ } = \dfrac{{PD}}{{BD}}$
We can easily see PABD is a rectangle so
AP = BD
$\tan {60^ \circ } = \dfrac{{PD}}{{AP}}$
From the figure we can see PD = h+25
$\tan {60^ \circ } = \dfrac{{h + 25}}{{AP}} = \sqrt 3 \\\ AP = \dfrac{{h + 25}}{{\sqrt 3 }} \to eqn.1 \\\$
From equation(1) and equation(2) , we get
$\sqrt 3 \left( {h - 25} \right) = \dfrac{{h + 25}}{{\sqrt 3 }} \\\ \Rightarrow 3\left( {h + 25} \right) = h + 25 \\\ \Rightarrow 3h + 75 = h + 25 \\\ \Rightarrow 2h = 100 \\\ \Rightarrow h = 50m \\\$
Therefore , the height of the cloud is 50 m from the water surface.