Question
Question: In the adjoining vector diagram, what is the angle between \(\overrightarrow{A}\) and \(\overrightar...
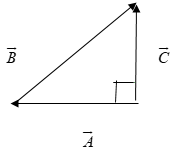
In the adjoining vector diagram, what is the angle between A and B?
(Given: C=2B)
A. 30∘
B. 60∘
C. 120∘
D. 150∘
Solution
When we’re given that the magnitude of the sum of two vectors is equal to half the magnitude of one of the vectors, the angle between the two vectors can be determined only if the ratio of the magnitudes of these two vectors is known.
We’re given a right triangle. Hence, we can use the basic trigonometric formulas to find the solution. In the given vector diagram, A is the base, B is the hypotenuse and C is the height. Note that A,B, and C are vectors and their direction should also be considered during calculation.
Formula used:
sinθ=BC, that is hypotenuseopp.side
Complete step by step answer:
Let θ be the angle between A and B.
From figure, sinθ=BC
We are given that, C=2B
Hence, sinθ=B(2B)
sinθ=21
⇒θ=sin−1(21)=30∘
Considering the direction of A and B, an obtuse angle is generated.
Hence, the angle between A and B is 180∘−30∘=150∘
So, the correct answer is “Option D”.
Note:
Most students tend to choose 30∘ as the answer as they consider it as a triangle and not a triangle composed of vectors. The direction is to be considered and the vectors are to be expanded along with the direction, so as to deduce the actual value of angles.
