Question
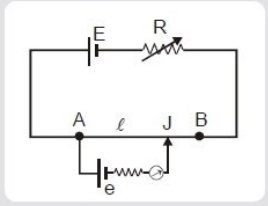
Question: In the adjoining potentiometer circuit, the resistance of uniform cross section the potentiometer wi...
In the adjoining potentiometer circuit, the resistance of uniform cross section the potentiometer wire AB of Length 1 m is 10Ω. When the variable resistance R=10Ω, the balance point is obtained for length l as shown. If the variable resistance is doubled, the new balance length is
A. l
B. 1.5l
C. 2l
D. 2l
Solution
The above problem can be solved using the mathematical relations that come under the potentiometer; the two conditions are given. The first condition is the specific value of the variable resistance, and the other condition is given for the double value of the variable resistance. Hence, the current can be identified using the formula and then substitute accordingly to obtain the final result
Complete step by step answer:
The length of the wire AB is, L=1m.
The value of the variable resistance is, R=10Ω.
Let E be the voltage of the main source and current in the circuit is,
I1=R+RE
When the variable resistance becomes double, then the above formula is expressed as,
