Question

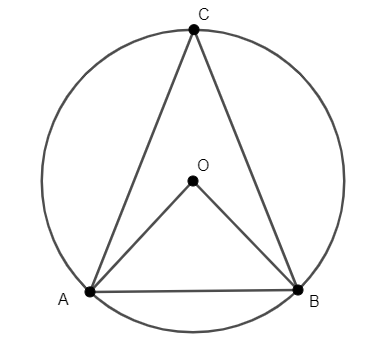
In the adjoining figure, in a circle with centre $O$, length of chord $AB$ is equal to the radius of the circle. Find the measure of arc $AB$

Answer 1

Hint: Find the value of the angle $\angle AOB$ of the triangle $\Delta AOB$. Use the formula that relates the arc length of any arc to the radius of the circle and the angle bisected by the arc at the centre of the circle.

Complete step by step answer:
We are given a circle with centre at $O$. $OA$ and $OB$ are the radii of the circle with centre $O$. The chord $AB$ of the circle has length equal to the radius of the circle. We want to find the measure of arc $AB$.

We will begin by observing that the triangle $\Delta AOB$ is an equilateral triangle as all of its sides have equal length that is equal to the radius of the circle.
Thus, the value of each angle of the triangle is equal to ${{60}^{\circ }}$. This is because; in an equilateral triangle all sides are equal. Thus, angles opposite to equal sides are also equal and the sum of all three angles of a triangle is ${{180}^{\circ }}$. Thus, the measure of each angle is ${{60}^{\circ }}$.
Hence, the measure of angle $AOB$ is $\angle AOB={{60}^{\circ }}$.
Now, we will use the formula that relates the arc length of any arc to the radius of the circle and the angle bisected by the arc at the centre of the circle.
In any circle, if an arc bisects an angle $\theta$ at the centre of circle whose radius is $r$, then the arc length of circle satisfies the equation $arclength=2\pi r\left( \dfrac{\theta }{{{360}^{\circ }}} \right)$.
In our case, we have $\theta ={{60}^{\circ }}$.

Hence, measure of arc AB$$$$=2\pi r\left( \dfrac{{{60}^{\circ }}}{{{360}^{\circ }}} \right)=2\pi r\left( \dfrac{1}{6} \right)=\dfrac{\pi r}{3}. We also take the measure of any arc as the angle subtended by the arc at the centre of the circle. Thus, we can write the measure of arc $AB=\dfrac{\pi r}{3}$.

Note: We can take the measure of the arc as the angle subtended by the arc at the centre of the circle or the length of the arc. It’s important to observe that $\Delta OAB$ is an equilateral triangle. It’s necessary to keep in mind the formula relating the arc length of any arc to the radius of the circle and the angle bisected by the arc at the centre of the circle.