Question
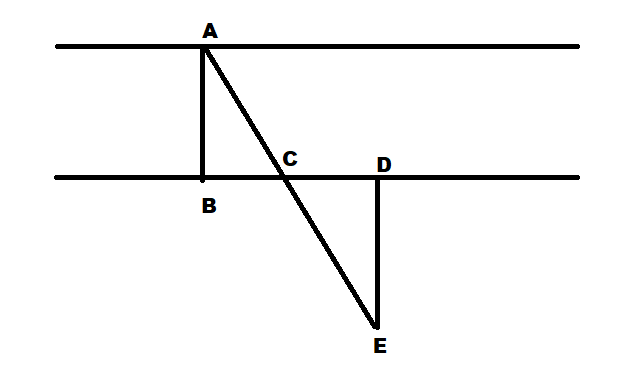
Question: In the adjoining figure, explain how one can find the breadth of the river without crossing it. The ...
In the adjoining figure, explain how one can find the breadth of the river without crossing it. The given figure attached with the question for detailing is:
Solution
Here the breadth of the river need to be calculated using the triangle, for which we need to find a relation between the sides, since only one angle of the triangle is known to us hence we cannot move with trigonometric identity, Pythagoras theorem is needed here.
Formulae Used: ⇒(hypotaneous)2=(base)2+(pendicular)2
Complete step-by-step solution:
The given question is to find the breadth of the river, without crossing the river. Here the breadth of the river can be calculated using the triangle given in the diagram; for upper triangle ABC in the diagram using Pythagoras rule for the right angle triangle, which states that:
For any right angle triangle ABC the square of length of hypotenuse is equal to the sum of squares of the length of the rest two sides of that triangle which is base and perpendicular.
If we derive the equation in mathematical form, we get:
Using the above expression we can derive for our given triangle, then breadth of the river can be given as:
⇒(AC)2=(AB)2+(BC)2 ⇒(breadth)2=(AC)2−(BC)2 ⇒breadth=(AC)2−(BC)2Note: Here for this question we can also use trigonometric function, in trigonometric function for a given angle we can find the relation between the sides of the triangle. Here we have to find the value of the perpendicular side for the given triangle, hence we can use either sin or cos function.
