Question

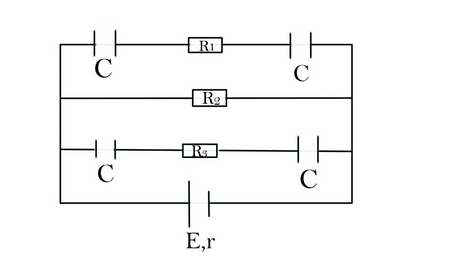
In the adjoining figure, $E = 5V$,$r = 1\Omega$, ${R_2} = 4\Omega$, ${R_1} = {R_3} = 1\Omega$ and $C = 3\mu F$. The numerical value of charge on each capacitor is

A. $3\mu C$
B. $6\mu C$
C. $12\mu C$
D. $24\mu C$

Answer 1

Hint: Capacitor will behave as a broken wire when it is fully charged.

Complete step-by-step answer:
Initially, the capacitor starts charging due to the potential difference across the capacitor. When the capacitor is fully charged, it behaves as a broken wire and the flow of current will stop in the wire in which the capacitor is connected.
So, in this case, the resistances ${R_1}$and ${R_3}$will not contribute to the resistance of the circuit because the current will not flow in that wire due to capacitors. The current will only flow in the ${R_2}$ resistor. So, the total resistance in the circuit will be
$R = {R_2} + r$
$R = 4 + 1 \\\ R = 5\Omega \\\$
Current in the circuit,
$I = \dfrac{E}{R}$
$I = \dfrac{5}{5} = 1A$
Potential difference across ${R_2}$
$V = I{R_2}$
$V = 1 \times 4 \\\ V = 4V \\\$
We can see that all the resistors in the circuit are parallel to each other which means that the potential difference will be the same across all the three.
Total capacitance in one branch
$= \dfrac{C}{2} = \dfrac{3}{2}\mu F$
We know that,
$Q = CV$
$Q = \dfrac{3}{2} \times 4 = 6\mu C$
b) is correct.

Additional information: In an AC circuit, capacitor reverses its charges as the current alternates and produces a lagging voltage (in other words, capacitor provides leading current in AC circuits and networks) Role of Capacitor in DC Circuits: In a DC Circuit, the capacitor once charged with the applied voltage acts as an open switch.

Note: The current does not flow through a fully charged capacitor because the potential difference across the capacitor becomes equal to the potential difference of the battery. Current does not flow between two points if the potential of the points are equal.