Question
Question: In the adjoining figure, capacitor (1) and (2) have a capacitance 'C' each. When the dielectric of d...
In the adjoining figure, capacitor (1) and (2) have a capacitance 'C' each. When the dielectric of dielectric constant K is inserted between the plates of one of the capacitors, the total charge flowing through battery is,
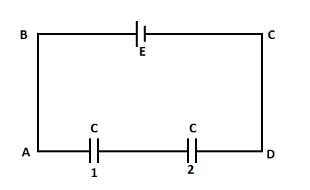
A. K+1KCEfrom B to C
B. K+1KCEfrom C to B
C. 2(K+1)(K−1)CEfrom B to C
D. 2(K+1)(K−1)CEfrom C to B
Solution
To solve the above problem we should know the effect of inserting the dielectric in between the capacitor. If the capacitance of a capacitor is C before inserting the dielectric then after inserting the dielectric of dielectric constant K the new capacitance will be C′=CK.
Complete answer:
Now to proceed with the solution of the given problem firstly we will calculate the equivalent capacitance of the circuit before inserting the dielectric.
Ceq=2C-----equation (1)
Now also we know that the formula for the charge stored in a capacitor,
So, the charge stored in the circuit having equivalent capacitance 2Cwill be,
Q=CeqV=2C×E
⇒Q=2CE-----equation (2)
Now after inserting the dielectric of dielectric constant Kin one of the capacitors.
Now the new capacitance of capacitor 2= C′=(dε0A)K
⇒C′=CK
So, the new equivalent capacitance will be,
Ceq′=C1+C′1
⇒Ceq′=C1+CK1
⇒Ceq′=C1(1+K1)
⇒Ceq′=C1(KK+1)
⇒Ceq′=K+1CK-----equation (3)
Now the stores charge in the circuit after inserting the dielectric will be,
So, the new charge Q′=Ceq′V=K+1CK×E
⇒Q′=K+1KCE--------equation (4)
Now the total charge flowing through the battery will be the difference between the earlier charge and the new charge in the circuit.
So, from the equation (1) form equation (4), we will get the total charge flowing through battery as follows,
So, Qtotal=Q′−Q
⇒Qtotal=(K+1KCE−2CE)
⇒Qtotal=CE[2(K+1)(2K−K−1)]
⇒Qtotal=2CE[(K+1)(K−1)]
And the charge will flow from the negative terminal of the battery to the positive terminal of the battery that is the opposite to the direction of the flow of the current.
So, the total charge flowing through battery is 2CE[(K+1)(K−1)]from C to B.
So, the correct answer is “Option D”.
Note:
The capacitor is an energy storing device used in a circuit. The stored energy in a capacitor is electrostatic potential energy and it is related to the charge Q and voltage V between the plates of the capacitor. A charged capacitor stores energy in the electrical field between its plates. When the capacitor is being charged, the electrical field builds up in between the plates and the energy is started to get stored.
