Question
Question: In the adjoining figure, \[\angle B={{90}^{\circ }}\], \[\angle BAC={{\theta }^{\circ }}\], \[BC=CD=...
In the adjoining figure, ∠B=90∘, ∠BAC=θ∘, BC=CD=4cm and AD=10cm. Find the value of cosθ.
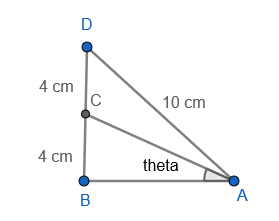
Solution
Hint: We will first again draw the figure given in the question and then we will apply the Pythagoras theorem twice to find the value of the missing side. And after this we will see the point from which we need to find the values and according to that we will select our base and hypotenuse.
Complete step-by-step answer:
Before proceeding with the question we should know the concept of Pythagoras theorem and right angled triangle.
A Right-angled triangle is one of the most important shapes in geometry and is the basics of trigonometry. A right-angled triangle is the one which has 3 sides, “base” “hypotenuse” and “height” with the angle between base and height being 90 degrees.
Pythagoras theorem states that “In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides“. The sides of this triangle have been named as Perpendicular, Base and Hypotenuse. Here, the hypotenuse is the longest side, as it is opposite to the angle 90 degree.
So we will first draw the figure given in the question.
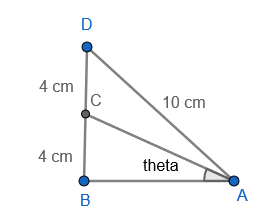
Now we will use Pythagoras theorem in ΔABD and from the figure we get,
⇒AD2=AB2+BD2........(1)
Now substituting the known values in equation (1) we get,
⇒102=AB2+82........(2)
Now rearranging the terms in equation (2) and then subtracting we get,
