Question

In the adjoining circuit, the battery ${E_1}$ has an E.M.F. of $12\,volts$ and zero internal resistance. While the battery ${E_2}$ has an E.M.F. of $2\,volts$ if the galvanometer $G$ reads zero than the value of the resistance $X$ in ohms is:

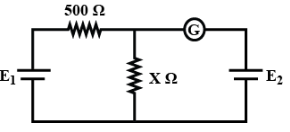
A. $10$
B. $100$
C. $14$
D. $200$

Answer 1

According to Kirchhoff’s voltage law (KVL), if you travel around any loop in a circuit, the voltages across the element add up to zero. That is in any closed path in a network, the algebraic sum of the $IR$ product is equal to the EMF in that path i.e, $\sum V = 0$. We will apply KVL in both the loops in order to get the desired result.

Complete step by step answer:

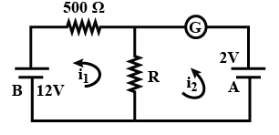
Let us consider the current flowing through loop (i) and (ii) be ${i_1}$ and ${i_2}$
Now the current flowing through the resistance $R$ well be $({i_1} - {i_2})$
Using Kirchhoff’s voltage law in loop (i) we get,
$\- 12 + X({i_1} - {i_2}) + 500{i_1} = 0 \\\ \Rightarrow X{i_1} - X{i_2} + 500{i_1} = 12......(1) \\\$
Now applying KVL in loop (ii) we get,
$2 + X({i_2} - {i_1}) = 0 \\\ \Rightarrow X{i_1} - X{i_2} = 2......(2) \\\$
Since current flowing through galvanometer is zero therefore, we can say
${i_2} = 0......(3)$
Using (2) and (3) we get,
$X{i_1} = 2......(4)$
Now using (4) and (3) in (1) we get,
2 + 500{i_1} = 12 \\\ \Rightarrow 500{i_1} = 10 \\\ \Rightarrow{i_1} = \dfrac{{10}}{{500}} \\\ \Rightarrow{i_1} = \dfrac{1}{{50}} \\\
Now using above result in equation (4) we get,
$X{i_1} = 2 \\\ \Rightarrow X \times \dfrac{1}{{50}} = 2 \\\ \therefore X = 100\Omega$
Hence the resistance of the resistor $R$ is $100\Omega$

Thus, option B is correct.

Note: While using KVL we have to keep in mind that the KVL equation is obtained by traversing a circuit loop in either direction and writing down unchanged the voltage of each element whose + terminal is entered first and writing down the negative of every element's voltage where the minus sign is first met. The loop must start and end at the same point.