Question
Question: In the adjoining circuit diagram each resistance is of 10 \[\Omega \]. The current in the arm AD wil...
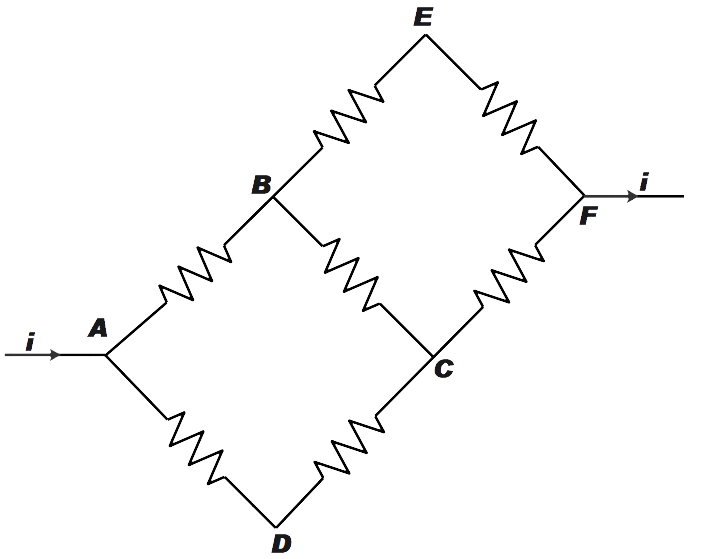
In the adjoining circuit diagram each resistance is of 10 Ω. The current in the arm AD will be.
A. 52i
B. 53i
C. 54i
D. 5i
Solution
In this question we have been given a circuit diagram and to calculate the value of current in the arm AD of the given circuit diagram. We have been given that the resistance of each resistor in the diagram is 10 ohms. Therefore, we shall be using Kirchhoff’s law and loop rule to solve this question. Kirchhoff’s loop rule suggests that the sum of potential difference in any loop must be zero.
Complete answer:
From the given diagram, it is said that every resistor has the resistance of 10 ohms. Let us assume that the voltage applied is V
Also, let the current in the arm AB, AD and BC be i1, i2 and i3 respectively. Now, from the diagram we can say that, the current through arm BE and CF is i1−i3 and i1+i2 respectively.
Now, let the potential at point A be V
From Kirchhoff’s law we know,
i=i1+i2
Now, we know that potential at point C must be equal.
Therefore, we can say
V−iR−i3R=V−2i2R
On solving
We get,
i1+i3=2i2
Now, we also know that potential at point should also be equal from both sides
Therefore,
V−iR−(i1−i3)2R=V−2i2R
On solving
We get,
i1+(i1−i3)2=2i2+(i1+i3)
Therefore,
3i1−2i3=3i2+i3
On solving
i1=i3+i2
After substituting the value of i3from
We get,
i1=2i2−i1+i2
Therefore,
2i1=3i2
Now, after substituting the value of i1 from
2i−2i2=3i2
On solving
We get,
i2=52i
So, the correct answer is “Option A”.
Note:
Kirchhoff’s loop rule also called as Kirchhoff’s Voltage law states that the sum of all the electric potential differences around a loop is zero. While applying the loop rule, we must first select a closed loop and decide the direction to go around the loop. The loop rule suggests that when a charge goes around a loop in a circuit and then returns to its starting point the potential energy of the charge must be the same as the charge is moving through the potential differences in the selected loop.
