Question
Question: In the adjoining circuit diagram, \(E=5V\), \(r=1\Omega \), \({{R}_{2}}=4\Omega \), \({{R}_{1}}={{R}...
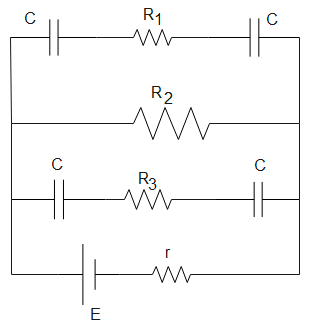
In the adjoining circuit diagram, E=5V, r=1Ω, R2=4Ω, R1=R3=1Ω and C=3μF. Then the numerical value of the charge on each plate of the capacitance is
(A). 20μC
(B). 12μC
(C). 6μC
(D). 3μC
Solution
The circuit shown contains capacitors as well as resistors connected together. As capacitors are assumed to be charged, no current flows through the arms containing the capacitors. The current only flows through the arms not containing the capacitors. We can use ohm’s law and the relation between charge, capacitance and potential to calculate charge on each capacitor.
Formulas used:
R=IV
C1=C11+C21
Q=CV
Complete answer:
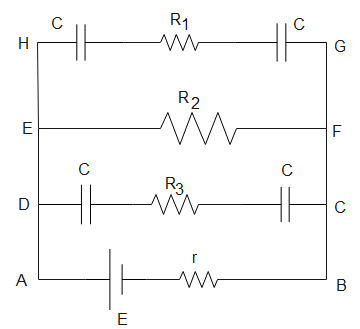
We assume that, t=∞ hence, the capacitors will act like open circuits and no current will flow through the arms containing the capacitors.
Total working resistance in the circuit will be R2+r. Given, R2=4Ω, E=5V, r=1Ω
According to Ohm’s law,
R=IV - (1)
Here, R is the resistance
V is the potential difference
I is the current in the circuit
Substituting given values in the above equation to get,
4+1=I5⇒I=55∴I=1A
Therefore, the current in the circuit is 1A.
The potential difference across R2 from eq (1) will be-
4=1V⇒V=4V
Therefore, the potential difference across R2 will be 4V.
Arms HG and DC are connected in parallel to R2, so their potential will be equal to R2.
Equivalent capacitance in the arm DC is calculated by using the equivalent capacitance connected in series, therefore,
C1=C11+C21
Given, C=3μF. Substituting given values in the above equation to get,
C1=31+31⇒C1=32∴C=23mF
Therefore, the equivalent capacitance is 23μF and the potential across each capacitor is 24=2V.
We know that,
Q=CV
Here, Q is the charge on the capacitor
C is the capacitance of the capacitor
V is the value of the potential difference between plates of capacitor
Substituting given values in the above equation to get,
Q=23μF×2V⇒Q=3μC
The charge on each capacitor will be the same and the magnitude of charge is 3μC.
Therefore, the magnitude of charge across each capacitor is 3μC.
Hence, the correct option is (D).
Note:
In series, the charge across each capacitor is the same whereas in parallel, the potential across each capacitor is the same. When the capacitor gets fully charged, it does not allow current to flow through it and hence acts like an open circuit. Since, the capacitance is the same on all capacitors, the potential in series will be distributed uniformly. That is why, potential on each capacitor is half of the total potential.
