Question

In the adjacent figure, a boy on a horizontal platform A, kept on a smooth horizontal surface, holds an attached rope to the box B. The boy pulls the rope with a constant force of 50N. The coefficient of friction between boy and platform is 0.5 (mass of boy = 80kg, mass of the platform = 120kg and the mass of box = 100kg)

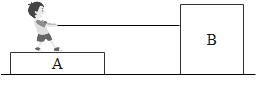
A) Velocity of platform relative to box after 4sec is 3m/s
B) Velocity of boy relative to platform after 4sec is 2m/s
C) Friction force between the boy and platform is 30N
D) Friction force between boy and platform is 50N

Answer 1

In the above question the boy pulls the rope with constant force of 50N. Hence the box will get pulled towards the boy as well as the tension in the rope will pull the boy towards the box. Hence we first need to obtain the relative acceleration of the boy and platform with respect to the box and using Newton’s first kinematic equation we can determine the relative speed of the boy and the box.

Formula used:
$F=ma$
${{v}_{rel}}={{u}_{rel}}+{{a}_{rel}}t$

Complete step-by-step answer:
In the above question initially the boy before pulling the rope, the relative velocity ${{u}_{rel}}$between the boy and the box is zero. As soon as the boy pulls the rope with force F = 50N, the box of mass m = 100kg, will move towards the boy and the platform. Hence from Newton’s second equation, the acceleration ${{a}_{B}}$ of the box will be,
$\begin{aligned} & F=m{{a}_{B}} \\\ & \Rightarrow 50N=100kg\times {{a}_{B}} \\\ & \therefore {{a}_{B}}=\dfrac{50}{100}Nk{{g}^{-1}}=0.5m{{s}^{-2}} \\\ \end{aligned}$
As the boy pulls the rope, the tension in the rope will pull the boy of mass A as well as the platform B towards the box. Hence the acceleration of the boy and the platform ${{a}_{P}}$from Newton’s second law is given by,
$\begin{aligned} & F=-(A+B){{a}_{P}} \\\ & \Rightarrow 50N=-(80+120)kg\times {{a}_{P}} \\\ & \therefore {{a}_{P}}=-\dfrac{50}{200}Nk{{g}^{-1}}=-0.25m{{s}^{-2}} \\\ \end{aligned}$
Hence the relative acceleration ${{a}_{rel}}$ of the boy and platform with respect to the box is,
$\begin{aligned} & {{a}_{rel}}={{a}_{B}}-{{a}_{P}} \\\ & \Rightarrow {{a}_{rel}}=0.5m{{s}^{2}}-(-0.25m{{s}^{2}}) \\\ & \therefore {{a}_{rel}}=0.75m{{s}^{2}} \\\ \end{aligned}$
Therefore from Newton’s first kinematic equation, the relative velocity ${{v}_{rel}}$ of the boy and the platform with respect to the box after t = 4sec from initial is equal to,
$\begin{aligned} & {{v}_{rel}}={{u}_{rel}}+{{a}_{rel}}t \\\ & \Rightarrow {{v}_{rel}}=0+0.75m{{s}^{-2}}\times 4s \\\ & \Rightarrow {{v}_{rel}}=3m{{s}^{-1}} \\\ \end{aligned}$

So, the correct answer is “Option A”.

Note: It is to be noted that the coefficient of friction between the boy and the platform is 0.5. Hence the frictional force (product of normal times the coefficient of friction)between the boy and the platform is 400N. The tension in the rope is 50N which is small then the frictional force. Hence they will remain in contact and move together.