Question

In the adjacent figure, a boy, on a horizontal platform A, kept on a smooth horizontal surface, holds a rope attached to a box B. The boy pulls the rope with a constant force of 50 N. The coefficient of friction between boy and platform is 0.5. (Mass of boy = 50 Kg, the mass of platform 120Kg, the mass of box = 100 Kg)

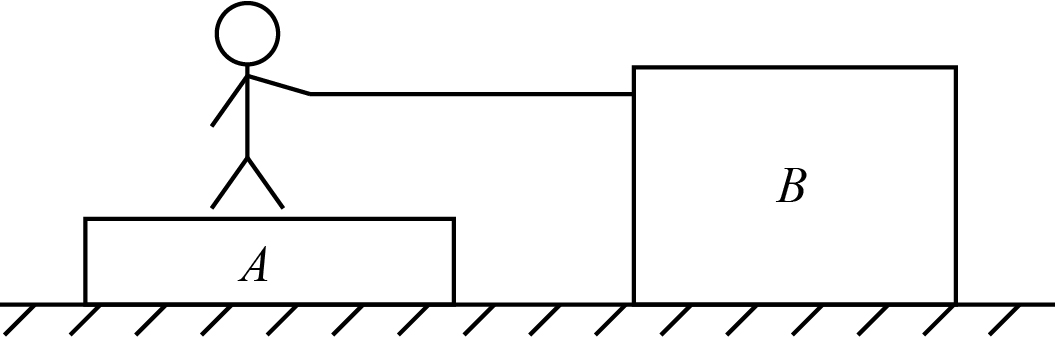
A. Velocity of platform relative to box after 4 s is 3 m/s.
B. The velocity of the boy relative to the platform after 4 s is 2 m/s.
C. The friction force between boy and platform is 40 N.
D. None of these

Answer 1

–In this question, it is given that the boy is pulling the rope, which is attached from block B, so the tension in the rope will be equal to the pull. You need to use Newton’s 2nd law to establish a relationship; with frictional force and relative motion analysis, you can determine the velocity of the platform relative to the box.

Complete step by step answer:
In this given question, the given quantities are,
Mass of boy
${m_{boy}} = 50\;{\rm{Kg}}$
The mass of the box ${m_b} = 100{\rm{ Kg}}$
The coefficient of friction between the boy and platform $\mu = 0.5$
The tension is the rope is equal to the pull of the boy, i.e., 50 N
So, by the free body diagram of platform A,

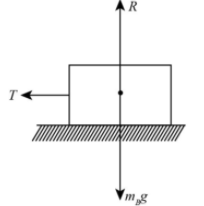
Applying Newton’s 2nd law
$T + {F_R} = {m_{boy}}{a_A}$
Where ${F_R} = \mu R$ is the frictional force acting between the platform and the boy.
Where R is the reaction force of the platform and $\mu$ is the friction coefficient.

T + \left( {0.5 \times \left( {120 \times g} \right)} \right) = 50{a_A}\\\ \Rightarrow 50 + 60 \times 10 = 50{a_A}\\\ \Rightarrow {a_A} = \dfrac{{650}}{{50}}\\\ \Rightarrow {a_A} = 13\;{\rm{m/se}}{{\rm{c}}^{\rm{2}}} \end{array}$$ So the acceleration of block A is $$13\;{\rm{m/se}}{{\rm{c}}^2}$$ For block B, tension is the only force acting on it, so from Newton’s 2nd law, $\begin{array}{l} T = {m_b}{a_B}\\\ \Rightarrow {a_B} = \dfrac{T}{{{m_b}}}\\\ \Rightarrow {a_B} = \dfrac{{50}}{{100}}\\\ \Rightarrow {a_B} = 0.5\;{\rm{m/se}}{{\rm{c}}^{\rm{2}}} \end{array}$ So, the acceleration of block A is $$\;0.5\;{\rm{m/se}}{{\rm{c}}^{\rm{2}}}$$ For block B (from the free body diagram) Acceleration of platform A relative to Block B ${a_{\dfrac{A}{B}}} = {a_A} + {a_B}$ $\Rightarrow {a_{\dfrac{A}{B}}} = 13 + 0.5 = 13.5\;{\rm{m/se}}{{\rm{c}}^{\rm{2}}}$ We added the acceleration because both the individual accelerations are in the opposite direction. For finding the acceleration with respect to plat from A, the addition of acceleration is considered from the relative motion analysis. At t=4 sec from Newton’s first equation, ${v_{\dfrac{A}{B}}} = u + {a_{\dfrac{A}{B}}}t$ So, $\begin{array}{c} {v_{\dfrac{A}{B}}} = 0 + 13.5 \times 4\\\ \Rightarrow {v_{\dfrac{A}{B}}} = 54\;{\rm{m/sec}} \end{array}$ **Hence, the velocity of platform A with respect to platform B is $54\;{\rm{m/sec}}$.** **Note:** You may go wrong in this question while calculating the relative acceleration because you need to understand the acceleration directions here, whether they need to be added or subtracted.