Question
Question: In the adjacent diagram, CP represents a wavefront and AO and BP, the corresponding two rays. Find t...
In the adjacent diagram, CP represents a wavefront and AO and BP, the corresponding two rays. Find the condition on !!θ!! for constructive interference at P between the ray BP and reflected ray OP.
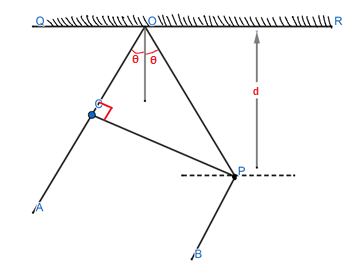
A. cosθ=2d3λB. cosθ=4dλC. secθ−cosθ=dλD. secθ−cosθ=d4λ
Solution
Hint: The two light rays that are interfering at point P are the waves BP and OP. So OP is a part of the original wavefront AO and OP is the reflected part of the wavefront AO. A light undergoing a reflection suffers a phase change of 180∘ or π. So, in order to create interference, the two waves interfering should be in phase. So, the path difference between these two waves should be an integral multiple of the wavelength.
Complete step-by-step answer:
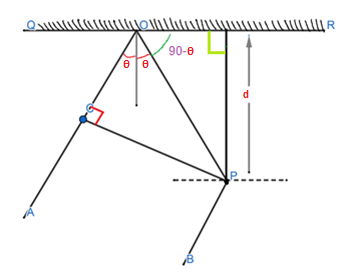
From the figure above we can understand that the ray OP had to travel an extra distance of CO and OP in order to reach point P. This extra distance is defined as the path difference between the two waves interfering at point P. Since there is a reflection taking place, there is an extra path difference of 2λ between the two waves which are interfering.
So, the condition for interference, in this case, is that the total path difference should be an integral multiple of 2λ. So, we can write,
Total Path Difference=n2λ
We know that the total path difference is the sum of distances CO and OP. So, we can write
CO+OP=n2λ … equation (1)
We can express OP as,
sin(90∘−θ)=OPd
∴OP=cosθd … equation (2)
After the value of OP, we can determine the value of CO as,
cos(2θ)=OPCO (∵∠COP=2θ)
⇒CO=OPCos(2θ)
Substituting the value of OP from equation (1) into the equation above,
∴CO=cosθdcos(2θ) … equation (3)
Substituting the values from equation (2) and equation (3) in equation (1), we get,
cosθdcos(2θ)+cosθd=2nλ
cosθd(2cos2θ−1)+cosθd=2nλ (∵cos2θ=2cos2θ−1)
cosθd(2cos2θ−1+1)=2nλ
∴2dcosθ=2nλ
Let n=1, so, the condition for interference can be written as,
cosθ=4dλ
So, the answer to the question is option (B).
Note: The condition for constructive interference for two light rays at a point P is given by the condition is given by, Δx=nλ, whereλ is the wavelength of light, Δx is the path difference. This relation means that two waves produce a constructive interference if the path difference between them is an integral multiple of the wavelength of light.
The condition for destructive interference for two light rays at a point P is given by the condition is given by, Δx=(2n+1)2λ, whereλ is the wavelength of light, Δx is the path difference. This relation means that two waves produce a destructive interference if the path difference between them is an integral multiple of half the wavelength of light.
