Question
Question: In the above question if the light incident is monochromatic and point O is a maxima, then the wavel...
In the above question if the light incident is monochromatic and point O is a maxima, then the wavelength of the light incident cannot be
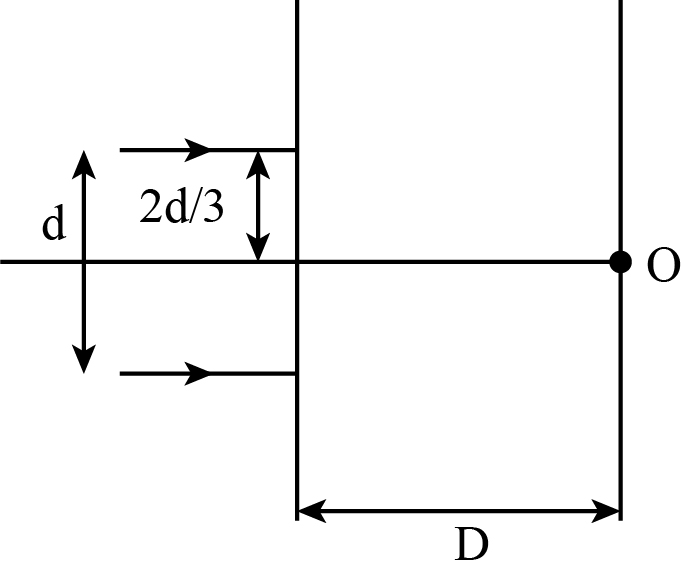
A. 3Dd2
B. 6Dd2
C. 12Dd2
D. 18Dd2
Solution
The above problem can be resolved using the concepts and the fundamental of the wavelength of light incident on a specific point, given the necessary condition that the incident light is the monochromatic light. The formula for the wavelength is used for the condition of the maximum obtained on the screen.
Complete step by step answer:
The path difference of the light incident on the point O is given as,
Dxd=nλ
Here, x is the path difference of the incident light, d is the distance between the slit or the slit width and the D is the distance between the slit and the screen, λ is the wavelength of light and n is the order of diffraction
The above relation can be standardised as in the form of,
nλ=6Dd2
For the maxima at point O, the value of n can be, n=1,2,3.
Substituting the values one by one in the above equation as,
