Question
Question: In the above figure, what is the net electric potential at point P due to the four particles if \( V...
In the above figure, what is the net electric potential at point P due to the four particles if V=0 at infinity, q=5.00fC and d=4.00cm ?
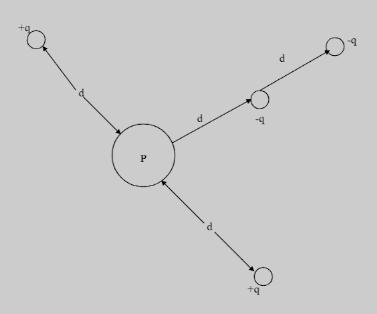
Solution
Electric field is a vector quantity, while electric potential is a scalar quantity. Thus, to find the electric potential on a point due to several other point charges, we could make a sum of their individual electric potential with respect to the point charge. So, to find the electric potential on point P due to the other point charges, we can find the electric potential of each point charge on P and add them, V=V1+V2+V3+V4 .
Formulas used We will be using the formula to find the electric potential of a point charge on a body given by, V=dkq , where V is the electric potential on a point by a point charge, q is the magnitude of the point charge, d is the distance between the charge and the point, and k is the electrostatic constant given by, k=4πε01 .
Complete Step by Step Solution
We can see that there are 4 charges surrounding the point P, in 3 directions. There are 2 point charges +q at a distance d in two opposite sides of point P, and a charge −q at a distance 2d from P, and another charge −q at a distance d from the point P in the same direction along the previously mentioned charge.
The electric potential of charges at either side of point P on P are given by,
V1=V2=dk(+q)
Similarly, the electric potential on point P, due to the third charge,
V3=2dk(−q)
And the electric potential on point P due to the fourth charge will be,
V4=dk(−q)
We know that electric potential is a scalar quantity, thus the total electric potential on point P is simply the sum of all the electric potentials on point P, V=V1+V2+V3+V4 .
Vtotal=dk(+q)+dk(+q)+2dk(−q)+dk(−q)
Vtotal=kq[d(+1)+d(+1)+2d(−1)+d(−1)]
Substituting the value of k=4πε01 and solving,
Vtotal=4πε01q[2d(2+2−1−2)]
Vtotal=4πε01q[2d(1)]
We also know that the q=5.00fC=5×10−15C , d=4.00cm=4×10−2m and the value of the electrostatic constant, k=4πε01=8.996×109Nm2C−2 .
Vtotal=8.996×109Nm2C−2×5×10−15C[2×4×10−2m(1)]
Solving for Vtotal we get,
Vtotal=5.5625×10−4Nm/C .
Note
The electric potential is a scalar quantity because it is a ratio of the potential energy of the system per unit charge, but the electric field is a vector because it is the ratio of the electric force applied to the distance.
