Question

In square $ABCD$ , side $AB$ has column vector \left( {\begin{array}{*{20}{c}} 2 \\\ 1 \end{array}} \right) . Find two possible column vectors for $\overrightarrow {BC}$ .

Answer 1

Hint : A column vector represents components of the vector written in a single column of a matrix. For a 2D vector two components of the vector are written. In this question we have been given a column vector for a side of a square. We have to find the possible column vectors for the adjacent side $BC$ . We can use the conditions that the side $BC$ will have the same length as side $AB$ , and it will also be perpendicular to the side $AB$ .

Complete step by step solution:
We have been the column vector of the side $AB$ of a square $ABCD$ . The column vector is given as \left( {\begin{array}{*{20}{c}} 2 \\\ 1 \end{array}} \right) .
We have to find two possible column vectors for the side $\overrightarrow {BC}$ .
We can convert column vector in component form as,
\overrightarrow {AB} = \left( {\begin{array}{*{20}{c}} 2 \\\ 1 \end{array}} \right) = 2i + j , where $i$ is the unit vector for x-axis and $j$ is the unit vector for y-axis.
The magnitude or length of side $AB$ is $\left| {\overrightarrow {AB} } \right| = \sqrt {{2^2} + {1^2}} = \sqrt {4 + 1} = \sqrt 5$
And the unit vector of side $AB$ is $\dfrac{{\overrightarrow {AB} }}{{\left| {\overrightarrow {AB} } \right|}} = \dfrac{{2i + j}}{{\sqrt 5 }} = \dfrac{2}{{\sqrt 5 }}i + \dfrac{1}{{\sqrt 5 }}j$
We can assume that the point $A$ lies on the origin. Then we can get the point $B$ as $\left( {2,1} \right)$ .
We know that the scalar product of two perpendicular vectors is zero.
Let us assume a unit vector $\dfrac{x}{{\sqrt {{x^2} + {y^2}} }}i + \dfrac{y}{{\sqrt {{x^2} + {y^2}} }}j$ that is perpendicular to side $AB$ .
Two such unit vectors may exist which will result in two different squares as shown in the figure below,

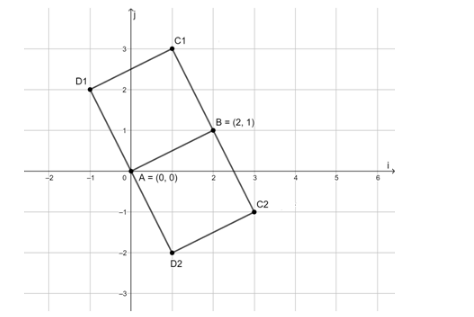
Since $\dfrac{x}{{\sqrt {{x^2} + {y^2}} }}i + \dfrac{y}{{\sqrt {{x^2} + {y^2}} }}j$ is perpendicular to side $AB$ , we have,
$\left( {\dfrac{x}{{\sqrt {{x^2} + {y^2}} }}i + \dfrac{y}{{\sqrt {{x^2} + {y^2}} }}j} \right).\left( {\dfrac{2}{{\sqrt 5 }}i + \dfrac{1}{{\sqrt 5 }}j} \right) = 0 \\\ \Rightarrow \dfrac{2}{{\sqrt 5 }}\dfrac{x}{{\sqrt {{x^2} + {y^2}} }} + \dfrac{1}{{\sqrt 5 }}\dfrac{y}{{\sqrt {{x^2} + {y^2}} }} = 0 \\\ \Rightarrow 2x = - y \\\ \Rightarrow x = - \dfrac{1}{2}y \;$
We can assume $y = 2$ . Then $x = - 1$ .
We get a unit vector $\dfrac{{ - 1}}{{\sqrt {{{\left( { - 1} \right)}^2} + {2^2}} }}i + \dfrac{2}{{\sqrt {{{\left( { - 1} \right)}^2} + {2^2}} }}j = - \dfrac{1}{{\sqrt 5 }}i + \dfrac{2}{{\sqrt 5 }}j$ that is perpendicular to side $AB$ .
One possible vector for $BC$ is represented by $B{C_1}$ . The unit vector is $- \dfrac{1}{{\sqrt 5 }}i + \dfrac{2}{{\sqrt 5 }}j$ and the magnitude is $\sqrt 5$ . Thus,
$\overrightarrow {B{C_1}} = \sqrt 5 \left( { - \dfrac{1}{{\sqrt 5 }}i + \dfrac{2}{{\sqrt 5 }}j} \right) = - i + 2j$
The column vector for side $B{C_1}$ is \left( {\begin{array}{*{20}{c}} { - 1} \\\ 2 \end{array}} \right) .
Again, we can assume $y = - 2$ . Then $x = 1$ .
We get another unit vector $\dfrac{1}{{\sqrt {{{\left( { - 1} \right)}^2} + {2^2}} }}i + \dfrac{{ - 2}}{{\sqrt {{{\left( { - 1} \right)}^2} + {2^2}} }}j = \dfrac{1}{{\sqrt 5 }}i - \dfrac{2}{{\sqrt 5 }}j$ that is perpendicular to side $AB$ .
Another possible vector for $BC$ is represented by $B{C_2}$ . The unit vector is $\dfrac{1}{{\sqrt 5 }}i - \dfrac{2}{{\sqrt 5 }}j$ and the magnitude is $\sqrt 5$ . Thus,
$\overrightarrow {B{C_2}} = \sqrt 5 \left( {\dfrac{1}{{\sqrt 5 }}i - \dfrac{2}{{\sqrt 5 }}j} \right) = i - 2j$
The column vector for side $B{C_1}$ is \left( {\begin{array}{*{20}{c}} 1 \\\ { - 2} \end{array}} \right) .
Hence, two possible column vectors for $\overrightarrow {BC}$ are \left( {\begin{array}{*{20}{c}} { - 1} \\\ 2 \end{array}} \right) and \left( {\begin{array}{*{20}{c}} 1 \\\ { - 2} \end{array}} \right) .

Note : We took squares on both sides of the given side $AB$ as both are possible. For the side $BC$ we have to ensure the conditions that it is perpendicular to side $AB$ and has the same magnitude as side $AB$ . We can see that in 2D only two values for $BC$ would be possible. Also, we can find the point $C$ as $\overrightarrow C = \overrightarrow {BC} + \overrightarrow B$ .