Question

In square ABCD; $A=\left( 3,4 \right)$ , $B=\left( -2,4 \right)$ and $C=\left( -2,1 \right)$ . By plotting these points on a graph paper, find the coordinates of vertex D. Also, find the area of the square.
(A) $D=\left( 3,1 \right)$ , Area = 25 sq. unit
(B) $D=\left( 3,1 \right)$ , Area = 36 sq. unit
(C) $D=\left( 3,-1 \right)$ , Area = 25 sq. unit
(B) $D=\left( 3,-1 \right)$ , Area = 36 sq. unit

Answer 1

First of all, assume that the coordinate of point D is $\left( x,y \right)$ . Now, plot the points $A=\left( 3,4 \right)$ , $B=\left( -2,4 \right)$ , $C=\left( -2,1 \right)$ , and $D=\left( x,y \right)$ on the coordinate axes. We can see that the side AB is parallel to the x-axis and the side AD is perpendicular to the side AB. We know the property that a line perpendicular to the line parallel to the x-axis has its slope equal to infinite. Now, calculate the slope of side AD and make it equal to infinite, $\dfrac{y-4}{x-3}=\infty$ . Then, get the value of x. Using the distance formula, $\text{Distance}=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$ , calculate the lengths of the sides AB and AD. Now, solve it further and calculate the value of y. Now, check for which coordinate of point D, the slope of the side CD is equal to zero.
We know the formula of the area of a square, Area = ${{\left( side \right)}^{2}}$ . Now, using the length of the side AB, calculate the area of the square.

Complete step by step answer:
According to the question, it is given that we have a square ABCD and coordinates of points A, B, and C are $\left( 3,4 \right)$ , $\left( -2,4 \right)$ , and $\left( -2,1 \right)$ .
The coordinate of point A = $\left( 3,4 \right)$ ……………………………………………(1)
The coordinate of point B = $\left( -2,4 \right)$ …………………………………………(2)
The coordinate of point C = $\left( -2,1 \right)$ …………………………………………..(3)
Now, let us assume that the coordinate of the point D is $\left( x,y \right)$ ……………………………………(4)
On plotting the points A, B, C, and D on the coordinate axes, we get
We can see that the line AB is parallel to the x-axis.
We know the property that all four the interior angles of a square are equal to $90{}^\circ$ .
Using this property we can say that the angles $\angle A,\angle B,\angle C$ , and $\angle D$ are equal to $90{}^\circ$ .

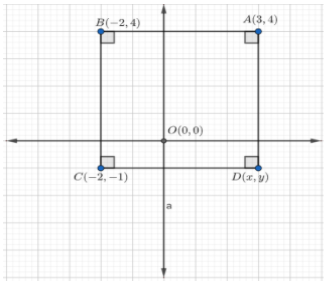
Since the points, A and B have their y coordinates equal so, we can say that the side AB is parallel to the x-axis.
From equation (1) and equation (4), we have the coordinates of points A and D.
The slope of the line AD = $\dfrac{y-4}{x-3}$ ……………………………………..(5)
We know the property that a line perpendicular to the line parallel to the x-axis has its slope equal to infinite …………………………………………..(6)
In the figure, we can observe that the side AD is perpendicular to the side AB ……………………………………..(7)
From equation (6) and equation (7), we can say that the slope of the line AD is equal to infinite ………………………………………..(8)
Now, from equation (5) and equation (8), we have

& \Rightarrow \dfrac{y-4}{x-3}=\infty \\\ & \Rightarrow \dfrac{y-4}{\infty }=x-3 \\\ & \Rightarrow 0=x-3 \\\ \end{aligned}$$ $$\Rightarrow 3=x$$ ………………………………………(9) From equation (1) and equation (2), we have the coordinates of points A and B. The coordinate of point A = $$\left( 3,4 \right)$$ , The coordinate of point B = $$\left( -2,4 \right)$$ . Using the distance formula, $$\text{Distance}=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$$ …………………………………………..(10) Now, the distance AB, $$\begin{aligned} & \Rightarrow AB=\sqrt{{{\left( 3-\left( -2 \right) \right)}^{2}}+{{\left( 4-4 \right)}^{2}}} \\\ & \Rightarrow AB=\sqrt{{{\left( 3+2 \right)}^{2}}} \\\ & \Rightarrow AB=\sqrt{25} \\\ \end{aligned}$$ $$\Rightarrow AB=5$$ ………………………………………………..(11) From equation (1) and equation (4), we have the coordinates of points A and D. The coordinate of point A = $$\left( 3,4 \right)$$ , The coordinate of point D = $$\left( x,y \right)$$ . Now, using equation (11), the distance AD, $$\Rightarrow AD=\sqrt{{{\left( 3-x \right)}^{2}}+{{\left( 4-y \right)}^{2}}}$$ …………………………………(12) Now, from equation (9) and equation (12), we get $$\Rightarrow AD=\sqrt{{{\left( 3-3 \right)}^{2}}+{{\left( 4-y \right)}^{2}}}$$ $$\Rightarrow AD=\sqrt{{{\left( 4-y \right)}^{2}}}$$ ……………………………………………………(13) We also know the property that all sides of a square are equal to each other. Using this property, we can say that the sides AB, BC, CD and AD are equal to each other. That is, $$AB=BC=CD=AD$$ …………………………………………….(14) From equation (11) and equation (13), we have the lengths of the sides AB and AD. Now, from equation (11), equation (13), and equation (14), we get $$\Rightarrow AB=AD$$ $$\Rightarrow 5=\sqrt{{{\left( 4-y \right)}^{2}}}$$ …………………………………..(15) $$\begin{aligned} & \Rightarrow 25=16+{{y}^{2}}-8y \\\ & \Rightarrow 25-16={{y}^{2}}-8y \\\ & \Rightarrow 9={{y}^{2}}-8y \\\ & \Rightarrow 0={{y}^{2}}-8y-9 \\\ & \Rightarrow 0={{y}^{2}}-9y+y-9 \\\ & \Rightarrow 0=y\left( y-9 \right)+1\left( y-9 \right) \\\ & \Rightarrow 0=\left( y+1 \right)\left( y-9 \right) \\\ \end{aligned}$$ So, $$y=-1$$ or $$y=9$$ ……………………………………….(16) Now, from equation (4), equation (9), and equation (16), we have The coordinate of point D is $$\left( 3,-1 \right)$$ or $$\left( 3,9 \right)$$ ……………………………………..(17) Since the line, AB is parallel to the x-axis so, the slope of line AB must be equal to zero. The lines AB and CD are parallel. So, the slope of the line AB and CD must be equal. Therefore, the slope of the line CD is equal to zero ………………………………………..(18) From equation (3) and equation (17), we have the coordinates of points C and D. For D = $$\left( 3,-1 \right)$$ , the slope of the line CD = $$\dfrac{-1-\left( -1 \right)}{3-\left( -2 \right)}=\dfrac{0}{5}=0$$ ……………………………………….(19) For D = $$\left( 3,9 \right)$$ , the slope of the line CD = $$\dfrac{-1-9}{3-\left( -2 \right)}=\dfrac{-10}{5}=-2\ne 0$$ ……………………………………….(20) But from equation (18), we must have the slope of the line CD equal to zero, and only for D = $$\left( 3,-1 \right)$$ , we the slope of the line CD equal to zero. So, the coordinate of point D is $$\left( 3,-1 \right)$$ …………………………………..(21) From equation (11), we have the length of side AB. We know the formula of area of a square, Area = $${{\left( side \right)}^{2}}$$ ……………………………………..(22) Now, from equation (11) and equation (22), we have The area of the square = $${{5}^{2}}=25$$ …………………………………………(23) Now, from equation (21) and equation (23), we have the coordinate of point D and the are of the square ABCD. Therefore, the coordinate of point D is $$\left( 3,-1 \right)$$ and the area of the square ABCD is 25 sq. units. **Hence, the correct option is (C).** **Note:** In this question, after getting the coordinates of point D, one might get confused and consider both the coordinates $$\left( 3,-1 \right)$$ and $$\left( 3,9 \right)$$ as the coordinates of point D. This is wrong because the side CD is also parallel to the side AB and the side AB also is parallel to the x-axis. We know that the slope of the x-axis is zero. So, the slope of the side AB and CD must also be equal to zero. Now, check for which coordinate of point D, the slope of the side CD is equal to zero.