Question
Question: In refraction incident ray and emergent ray are parallel. Type 1 for true and 0 for false....
In refraction incident ray and emergent ray are parallel. Type 1 for true and 0 for false.
Solution
To answer this question, we need to take the case of refraction through a glass slab. Then we need to examine whether the emergent ray is parallel to the incident ray, using Snell's law.
Formula Used: The formula used in this solution is
μ=sinrsini, μ=refractive index, i=angle of incidence, and r= angle of refraction
Complete step-by-step answer
Consider a glass slab of refractive index μ as shown in the flowing figure.
A ray AB is incident on the upper interface at the point C, which gets refracted in the glass medium as the ray CD. The refracted ray is incident on the lower interface at the point E. Finally, CD is refracted and emerges out of the glass medium back into the air as the rayEF.
Applying Snell’s law on the upper interface, we get
μ=sinrsini (i)
Again applying Snell’s law on the lower interface, we get
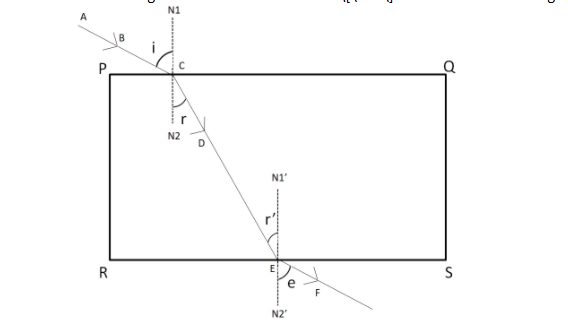
μ=sinr′sine (ii)
As N1N2 is the normal to the upper interface,
∴N1N2⊥PQ (iii)
Also, N’1N’2 is the normal to the lower surface
∴N’1N’2⊥RS (iv)
Case 1
If PQ∥RS then by (iii) and (iv), we have
N1N2∥N’1N’2
Now, in the figure, as r and r′ are alternate interior angles, so they are equal.
∴r=r′
Taking sine both the sides, we get
sinr=sinr′ (v)
From (i) and (ii)
sinrsini=sinr′sine
Multiplying with sinr on both sides
sini=sinrsinr′sine
From (v)
sini=sine
∵ both i&e are acute, so we can say
i=e
As N1N2∥N’1N’2 and i=e
So AB∥EF
Hence, the incident ray and emergent ray are parallel.
Case 2
If PQ&RS are not parallel, then
r=r′
both i&e are acute, so we can say
sinr=sinr′
From (i) and (ii)
sinrsini=sinr′sine
But sinr=sinr′
So, sini=sine and therefore
i=e
Thus, AB is not parallel to EF
∴ We conclude that the incident and the emergent rays are parallel only with the condition that the two refracting interfaces should be parallel to each other. They are not always parallel.
So the statement given in the question is false.
Hence, the correct answer is 0.
Note: This question can also be attempted by taking the case of refraction through a triangular prism. In that case, we can directly conclude that the emergent ray is not parallel to the incident ray through simple observation.
