Question
Question: In Process one, the energy stored in the capacitor \( {E_C} \) and heat dissipated across resistance...
In Process one, the energy stored in the capacitor EC and heat dissipated across resistance ED are related by:
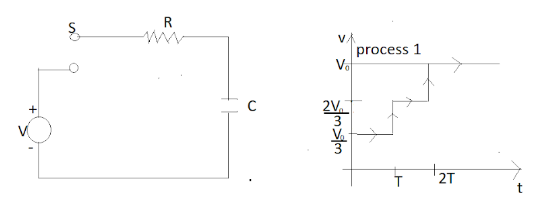
Solution
Hint : The capacitor always starts with zero voltage and it goes till full charge gradually to its full voltage. Energy stored in the capacitor finally is EC . Energy stored in a capacitor,
E = \dfrac{1}{2}C{V_0}^2 \\\
= \dfrac{1}{2}Q{V_0} \\\
Complete Step By Step Answer:
In order to solve this we first see the diagram, as the switch S is closed till time zero and the capacitor is fully charged to voltage V0 , some dissipation of energy occurs across the resistance. Energy stored in the capacitor finally is EC .
{W_b} = C{V^2} \\\
{E_C} = \dfrac{1}{2}C{V^2} \\\
For the energy stored in the capacitor and total energy stored in this process.
The capacitor always starts with zero voltage and it goes till full charge gradually to its full voltage.
Now work done by a battery;
W=QV0
Where V0 is the voltage across the battery?
Energy stored in a capacitor,
E = \dfrac{1}{2}C{V_0}^2 \\\
= \dfrac{1}{2}Q{V_0} \\\
Work done by a battery is divided by energy stored in the capacitor and operational energy.
Q{V_0} = {E_D} + \dfrac{1}{2}Q{V_0} \\\
{E_D} = \dfrac{1}{2}Q{V_0} \\\
Now energy stored in the capacitor is equal to the energy dissipated.
EC=ED
Also we can solve it like,
Final charge of the capacitor CV
So,
{W_b} = C{V^2} \\\
{E_C} = \dfrac{1}{2}C{V^2} \\\
{E_D} = {W_b} - \vartriangle {E_C} \\\
= C{V^2} - \dfrac{1}{2}C{V^2} \\\
= \dfrac{1}{2}C{V^2} \\\
{E_C} = {E_D} \\\
Hence option B is the correct answer.
Note :
The capacitor always starts with zero voltage and it goes till full charge gradually to its full voltage.
Now energy stored in the capacitor is equal to the energy dissipated. Work done by a battery is divided by energy stored in the capacitor and operational energy.
Q{V_0} = {E_D} + \dfrac{1}{2}Q{V_0} \\\
{E_D} = \dfrac{1}{2}Q{V_0} \\\
