Question

In order to raise a mass of 100kg a man of mass 60 kg fastens a rope to it and passes the rope over smooth pulley. He climbs the rope with an acceleration $\dfrac{{5g}}{4}$ relative to rope. The tension in the rope is: $\left( {g = 10m{s^{ - 2}}} \right)$ A. 1432 N B. 928 N C. 1218 N D. 624 N

Answer 1

The tension is defined as the axial reaction force generated by the string, cable or a one-dimensional object due to its extension. In this problem, the tension generated due to both the man and the mass exerting its weight, is equal. This can be determined by the free-body diagrams of both the objects.

Complete step-by-step solution:
Consider the pulley system with a rope whose one end is fastened to the mass of 100 kg and the man of 60 kg climbs the rope in the upward direction.

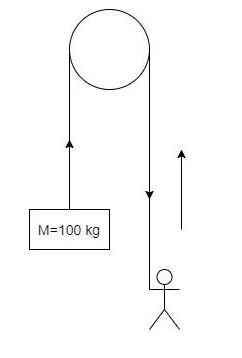
A free-body diagram must be drawn for both the mass and the man. The free-body diagram only represents the forces acting on the mass.

Free-body diagram of mass, M –

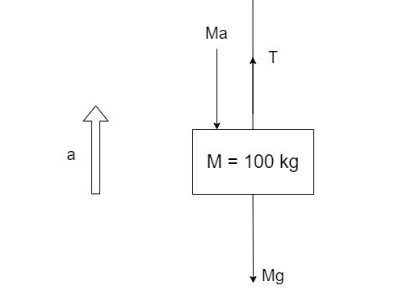
There are three forces acting on the mass M: i) Weight, Mg ii) Tension in the rope, T iii) Force acting due to acceleration in the opposite direction of acceleration and equal to the mass times the acceleration, Ma
By equilibrium,

$Ma + Mg = T$

Free-body diagram of man of mass m –

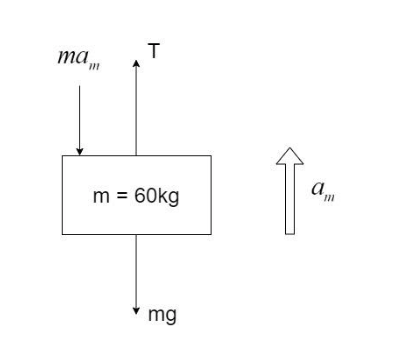
The man is moving at an acceleration equal to ${a_m}$
There are three forces acting on the man of mass m: i) Weight, mg ii) Tension in the rope, T iii) Force acting due to acceleration in the opposite direction of acceleration and equal to the mass times the acceleration, $m{a_m}$
By equilibrium,
$m{a_m} + mg = T$
From above equations, we have –
$m{a_m} + mg = Ma + Mg$
In the problem, it is given that the acceleration of the man relative to acceleration, $A = \dfrac{{5g}}{4}$
The relative acceleration of the man with respect to the block is given by –
$A = a + {a_m}$
The acceleration is added since the accelerations are in the same direction.
$a = A - {a_m}$
Substituting the values in the equation, we obtain –
$m{a_m} + mg = Ma + Mg$
$m{a_m} + mg = M\left( {A - {a_m}} \right) + Mg$
$\Rightarrow m{a_m} + mg = MA - M{a_m} + Mg$
$\Rightarrow 60 \times {a_m} + 60 \times g = 100 \times \dfrac{{5g}}{4} - 100 \times {a_m} + 100 \times g$
$\Rightarrow 160{a_m} = 125g + 40g$
$\Rightarrow 160{a_m} = 165g$
Given the value of $g = 10m{s^{ - 2}}$ ,
${a_m} = \dfrac{{1650}}{{160}} = 10 \cdot 312m{s^{ - 2}}$
Substituting the value of ${a_m}$ , we get –
$m{a_m} + mg = T$
$T = 60 \times 10 \cdot 312 + 60 \times 10 = 60\left( {20 \cdot 312} \right) = 1218 \cdot 72N$
Hence, the tension in the rope = 1218 N

Hence, the correct option is Option C.

Note: In this problem, it is mentioned as smooth pulley. This means that there is no frictional force acting on the rope, which is the ideal case. In real scenarios, the coefficient of friction between the pulley and rope must be taken into consideration while applying the equations.