Question

In non-inertial frame, the second law of motion is written as
$\begin{aligned} & (a)\,F=ma \\\ & (b)\,F=ma+{{F}_{p}} \\\ & (c)\,F=ma-{{F}_{p}} \\\ & (d)\,F=2ma \\\ \end{aligned}$
Where ${{F}_{p}}$ is a pseudo-force while $a$ is the acceleration of the body relative to a non-inertial frame.

Answer 1

In non-inertial frame, a pseudo force acts in the body in the opposite direction of the acceleration of the frame, which will reduce the force that is applied on the body, due to which the movement of the body will depend mainly on force applied and the pseudo force that is applied due to the non-inertial frame.

Complete answer:
In non-inertial frame, there is a force acting in the opposite direction of the body, known as pseudo-force, which reduces the overall force applied to the body, the force that is applied to the body and the pseudo force that is acting on it is shown below in the diagram:

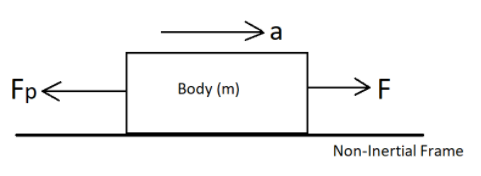
Here,
$a$ is Acceleration,
$F$ is Force, and
${{F}_{p}}$ is Pseudo Force.
The equation that can be depicted from above diagram is shown below:
$\begin{aligned} & \overrightarrow{F}=\overrightarrow{ma}+\overleftarrow{{{F}_{p}}} \\\ & \overrightarrow{F}=\overrightarrow{ma}-\overrightarrow{{{F}_{p}}} \\\ \end{aligned}$
If we remove the vector, then the equation can be written as:
$F=ma-{{F}_{p}}$

Therefore, the correct answer is Option (c).

Additional Information:
A non-inertial reference frame is a frame of reference that is undergoing acceleration with respect to an inertial frame. An accelerometer at rest in a non-inertial frame will, in general, detect a non-zero acceleration. While the laws of motion are the same in all inertial frames, in non-inertial frames, they vary from frame to frame depending on the acceleration.
In classical mechanics it is often possible to explain the motion of bodies in non-inertial reference frames by introducing additional fictitious forces (also called inertial forces and pseudo-forces) to Newton's second law. Common examples of this include the Coriolis force and the centrifugal force. In general, the expression for any fictitious force can be derived from the acceleration of the non-inertial frame. As stated by Goodman and Warner, "One might say that F = ma holds in any coordinate system provided the term 'force' is redefined to include the so-called 'reversed effective forces' or 'inertia forces'."

Note:
In an inertial frame, the second law of motion is written as $F=ma$. But the question has clearly stated that the frame is a non-inertial frame, so this will affect the force value, which will change the second law of motion for this frame.