Question

In modified YDSE setup $SS_1 - SS_2 = \frac{\lambda}{4}$ where $\lambda$ is wavelength of light used. $S_1$ & $S_2$ are two slits separated by distance $d$. A screen is placed at distance $D (D>> d>> \lambda)$. Source is also placed at distance $D$ from slits asymmetrically such that source $S$ is below the central line $CC'$. ($CS_1 = S_2C$). If point $P$ is corresponding to central maxima then angle $\theta$ is

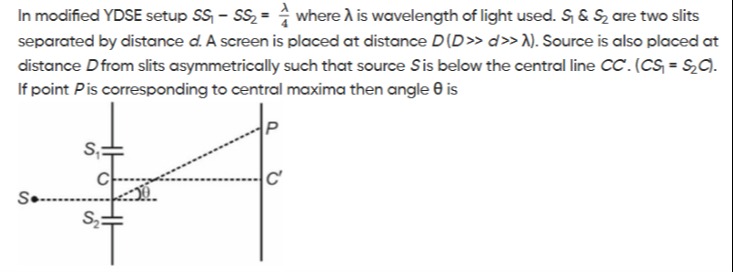
Answer 1

$\theta = \sin^{-1}\left(\frac{\lambda}{4d}\right)$

Answer 2

1. The source introduces an initial path difference so that

$$SS_1 - SS_2 = \frac{\lambda}{4} \quad \Longrightarrow \quad \phi_0 = \frac{2\pi}{\lambda}\cdot\frac{\lambda}{4} = \frac{\pi}{2}.$$

2. On the screen at an angle $\theta$, the extra path difference from the slits is

$$\delta = d\sin \theta \quad\Longrightarrow\quad \phi = \frac{2\pi}{\lambda}\,d\sin\theta.$$

3. For the resultant phase difference to yield a central maximum (bright fringe), the total phase difference must be zero modulo $2\pi$. That is, for the principal maximum,

$$\frac{2\pi}{\lambda}\,d\sin \theta - \frac{\pi}{2} = 0.$$

4. Solving for $\theta$:

$$\frac{2\pi}{\lambda}\,d\sin \theta = \frac{\pi}{2} \quad \Longrightarrow \quad d\sin\theta = \frac{\lambda}{4} \quad \Longrightarrow \quad \theta = \sin^{-1}\left(\frac{\lambda}{4d}\right).$$

Minimal Explanation

The initial phase difference from the source is $\pi/2$. For maximum, the additional phase difference from the path difference $d\sin\theta$ must cancel this, leading to $d\sin\theta=\lambda/4$ and hence $\theta=\sin^{-1}(\lambda/(4d))$.