Question

In meter bridge experiment, with a standard resistance in the right gap and a resistance coil dipped in water (in a beaker) in the left gap, the balancing length obtained is $l$. If the temperature of water is increased, the new balancing length is
A. $> l$
B. None
C. $= 0$
D. $= l$

Answer 1

To solve this question, we have to first deduce the relationship between the resistance and the temperature. When we apply this relation for the resistance in the meter bridge, we can obtain the change in the resistance when the temperature has changed.
The formula for the change in resistance with the temperature change $\Delta T$ is given by –
$R = {R_0}\left( {1 + \alpha \Delta T} \right)$
where ${R_0}$ is the resistance at reference temperature, $\alpha$ is the temperature coefficient of resistance of a material.

Complete step by step solution:
To understand the working of the meter bridge, the concept of Wheatstone’s network should be explained.
Consider the following network of four resistors A, B, C and D as arranged in the Wheatstone’s bridge with G as the galvanometer

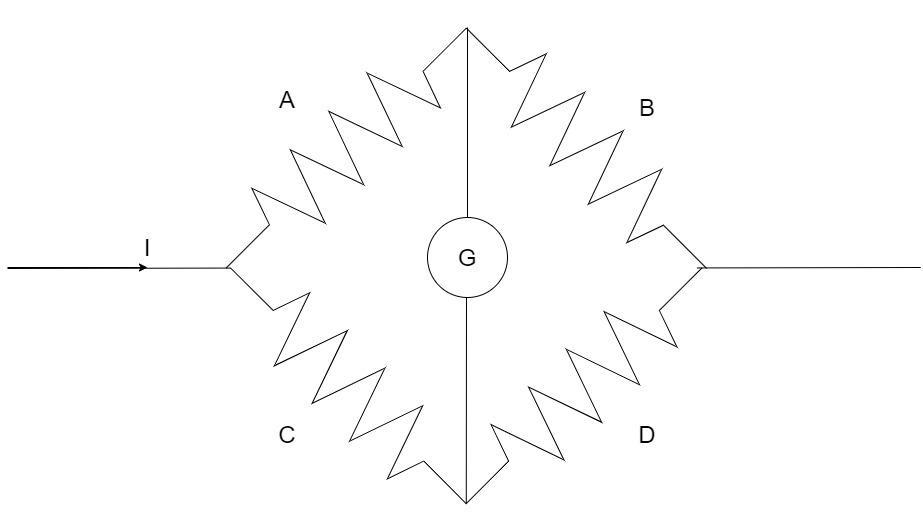
The galvanometer is said to be balanced if there is no current flowing through the galvanometer G in the figure. This can be achieved by having the 4 resistances in the following ratio:
$\dfrac{A}{B} = \dfrac{C}{D}$
This arrangement can be extended to a device known as metre bridge which can be used to calculate the unknown resistance.
The metre bridge consists of a wire of length 1 metre, which is pinned on both ends to a circuit. There are two slots for introducing resistances. On the left, the unknown resistance R, should be placed and the right, the standard known resistance S, should be placed.

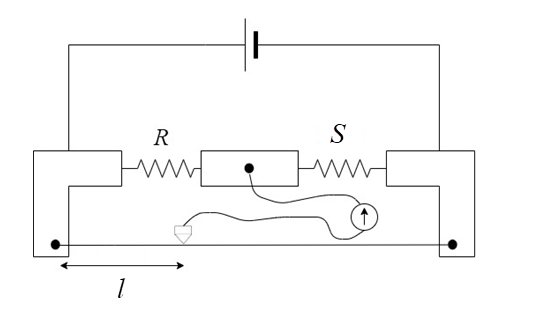
The jockey is a device which is connected to the galvanometer, which slides on the wire. At a length called the balancing length $l$, the galvanometer shows zero deflection and the value of the unknown resistance can be measured by the formula :
$\dfrac{R}{S} = \dfrac{l}{{1 - l}}$
As per the question, the resistance R is dipped in a beaker of water. When the temperature of the water rises, the resistance variation is given by –
$R = {R_0}\left( {1 + \alpha \Delta T} \right)$
Since, the coil is made of metal and metals have positive value of $\alpha$, we can say –
$R \propto T$
So, we can say that the resistance R increases with the temperature.
From the balance equation of the meter bridge, we get –
$\dfrac{R}{S} = \dfrac{l}{{1 - l}}$
$R \propto l$
Now, given that the resistance R, increases, the new balancing length will increase.
Thus, the new balancing length will be greater than the original $l$.

Hence, the correct option is Option A.

Note: Students can, often, get confused between R and S in the formula. Always, note that the known resistance will be in the denominator as it is connected on the left. So, the known resistance S will be equivalent to $\left( {1 - l} \right)$. If that is the case, then the unknown resistance will always be equivalent to the length of balance of the metre bridge, $l$.